This article was published in the Journal of Political Economy, and is webbed with their permission. I am working from the draft on my hard disk, so it may not be identical to the published version.

Cold Houses in Warm Climates and Vice Versa:

A Paradox of Rational Heating

David Friedman

A. B. Freeman School of Business

Tulane University

Abstract

Houses in cold climates are kept warmer in winter than those in warm climates, despite the greater cost of heating in colder climates. It is shown that this is not only consistent with but implied by rationality. The contrary intuition is based on a confusion between average and marginal cost. The same analysis implies that it is rational to keep the thermostat setting constant throughout the heating season, rather than changing it with changes in external temperature.

Cold Houses in Warm Climates and Vice Versa:

A Paradox of Rational Heating*

I. Introduction

A native of Chicago who spends a winter in Los Angeles or Canberra is likely to find the houses uncomfortably cold, and to express surprise that the natives are too stingy to heat their houses properly even though it would cost very little to do so. An Angelino wintering in Chicago or the Northeast is likely to have the opposite reaction; why, he wonders, do the inhabitants of such ferocious climates spend a fortune on overheating?

The pattern suggested by such casual observation--an inverse relation between external and internal temperature--seems inconsistent with rational behavior. The purpose of this note is to argue the opposite. Rational behavior, under the simplest and most obvious assumptions, implies that houses in warm climates will be colder than houses in cold climates.

I. Assumptions

The argument begins with one assumption in physics and several in economics. The physical assumption, which will be relaxed later in the paper, is that the only form of heat loss that need be taken into account is conduction; convection and radiation are assumed to be insignificant. The reason why this assumption greatly simplifies the argument will shortly become apparent.

The economic assumptions are that people living in different climates have the same utility function, that one of the arguments in that function is the temperature of the interior environment, that the marginal utility of interior warmth is independent of exterior warmth, that real income is equalized across climates by migration, and that fuel costs do not vary systematically with climate.

The failure of the first of these assumptions might well imply the opposite of the behavior I have described. It is plausible that people who have a taste for cold climates tend to live in them and that a taste for warmth outside correlates with a taste for warmth inside. If so, that would be a reason for houses to be warm in California and cold in Chicago; if, as I claim, the reverse is true, that may be taken as empirical evidence that other effects are stronger.

One could imagine violations of the third assumption, that the marginal utility of interior warmth is unrelated to external temperature, going in either direction. The warm interior of a Chicago home might increase the shock of stepping out into a Chicago winter; it also might be just what one would want after coming in from a Chicago winter. I prefer to simplify the problem by assuming that neither is true--that a cold climate neither increases nor decreases the utility of a warm house. One could perhaps find empirical evidence on the subject by comparing, in both warm and cold climates, the temperature of buildings whose inhabitants spend little time outdoors in the winter--nursing homes, for example--with the temperatures of buildings of which the opposite is true.

The final assumption, that real incomes are equalized by migration, is plausible as long as individuals correctly predict the costs associated with different climates. A sudden and unexpected change in such costs would increase the relative value of immobile assets, such as houses and location specific human capital, in one region and decrease them in another, producing a temporary real income differential; the consequences for the predictions of the model will be discussed.

II. The Proof

In order to maintain a house at a temperature T_i, it is necessary to put heat into the house as fast as it flows out. I shall assume for the moment that the resident faces a constant price of heat, P_h. Hence if U(T_i,X) is the resident's utility function, with X representing expenditure on all other goods, and if H(Ti,To) is the heat flow required to maintain the house at an interior temperature Ti when the exterior temperature is To, utility maximization implies that:

U₁/U₂ = P_h dH/dT_i (Equation 1)

To find dH/dT_i, we need only know that the rate at which heat flows through a barrier is proportional to the temperature difference between the two sides of the barrier, with the coefficient depending on the insulating qualities of the barrier. Hence:

H(T_i,T_o) = C. (T_i-T_o)

Where C depends on the size, shape, and insulation of the house. Hence:

dH/dT_i = C

Inserting this into equation 1 and solving for Ti, we find that Ti is independent of To! Putting the same argument into words, since heat loss by conduction is proportional to the temperature difference between outside and inside, the marginal cost of interior temperature--the cost, say, of keeping the house at 70 instead of 69, or at 65 instead of 64--depends on the characteristics of the house but is independent of both inside and outside temperature.¹ A utility maximizing resident will choose that temperature for which the marginal utility of an additional degree is just equal to its cost; since the cost is independent of outside temperature so is the optimal inside temperature.

What I have shown so far is that identical houses will be heated to the same temperature whatever the temperature outside (I ignore outside temperatures higher than the desired inside temperature, since I am only considering the temperature of houses in winter).² To finish the argument, it is only necessary to note that C, the marginal cost in heat flow of internal temperature, depends on characteristics of the house such as insulation and size. Since the total cost of heating is proportional to C. (T_i-T_o), where T_o is the average outside temperature throughout the year (ignoring months when T_o>T_i), and since C will be chosen (when the house is constructed) in such a way that the marginal benefit of decreasing it is equal to the marginal cost, it follows that C is a decreasing function of T_i-T_o; houses in Chicago should be (and are) better insulated than houses in Los Angeles.³

If, as argued above, identical houses will tend to have the same interior temperature in both cities, then for houses that differ in C, the optimal T_i will be higher the lower C is. Houses in Chicago will tend to be better insulated than houses in Los Angeles, and better insulated houses will be kept at a higher internal temperature. Hence warm houses are found in cold climates and vice versa.

III. The Formal Proof

The consumer has a utility function U(T_i,X), where T_i is internal temperature and X is expenditure on all other goods. U generates a set of indifference curves I1, I2, ... which are assumed convex to the origin, as shown in Figure 1. Internal temperature is constant over time, for reasons explained above.

The consumer is subject to a budget constraint:

W-r=X+Z+P_t(Z)(T_i-T_o); (Equation 2)

Here W is wage, r is land rent, Z is expenditure on insulation, P_t(Z)=CxP_h is the price of internal temperature and T_o is the average external temperature. I assume that external temperature is always lower than internal temperature.⁴

Since Z appears only in Equation 2, not in the utility function, we start by rewriting Equation 2 as:

W-r=X+C (Z,T_i-T_o) (Equation 2')

and minimizing

C (Z,T_i-T_o) Z+P_t(Z)(T_i-T_o) . (Equation 3)

Since P_t(Z) is the cost of increasing internal temperature, which is always positive and decreases with increasing insulation, we have:

dP_t(Z)/dz < 0; P_t(Z)>0

We then prove the following:

Lemma: If Z₁* minimizes C(Z,T₁) and Z₂* minimizes C(Z,T₂) and T₁>T₂, then Z₁*>Z₂*

Proof: Since Z₁* minimizes C(Z,T₁), we have:

C(Z₁*,T₁)<= C(Z₂*,T₁)

Similarly, since Z₂* minimizes C (Z,T₂), we have:

C (Z₂*,T₂)<= C (Z₁*,T₂)

Substituting from Equation 3 and adding the two inequalities, we have:

Z₁*+P_t(Z₁*)(T₁)+Z₂*+P_t(Z₂*)(T₂)<= Z₂*+P_t(Z₂*)(T₁)+Z₁*+P_t(Z₁*)(T₂)

P_t(Z₁*)(T₁-T₂)<= P_t(Z₂*)(T₁-T₂)

P_t(Z₁*)<= P_t(Z₂*)

Z₁*>= Z₂* Q.E.D.

Looking back at Equation 3, we see that the budget lines must have the shape shown in Figure 1. The higher T_i-T_o is, the larger Z*. The larger Z*, the smaller P_t(Z*). But the slope of the budget line is simply -1/P_t(Z*), hence the budget line gets steeper as Ti gets higher. In other words, the larger the desired temperature differential between inside and outside, the larger the optimal amount of insulation, and the smaller the cost of an additional degree of internal temperature.

Defining Z*(T_i-T_o) as the value of Z that minimizesC, Equation 2 reduces to:

W-r=X+Z*(T_i-T_o)+P_t(Z*(T_i-T_o))(T_i-T_o)

=X+Z*(T_i-T_o)+C (Z*(T_i-T_o),(T_i-T_o)); (Equation 2'')

We are now ready to prove:

Theorem: Let T_i1,X₁ maximize U(T_i,X) subject to the budget constraint:

W₁-r₁=X1+Z*(T_i1-T_o1)+P_t(Z(T_i1-T_o1))(T_i1-T_o1)

and similarly for T_i2,X₂,W₂,r₂,T_o2 .

If T_o2>T_o1 and U(T_i1,X₁)=U(T_i2,X₂) then T_i1>= T_i2 .

Here the individual is setting Ti, Z and X to maximize utility; migration adjusts wages and rents⁵ in the two locations to make U(T_i1,X₁)=U(T_i2,X₂).

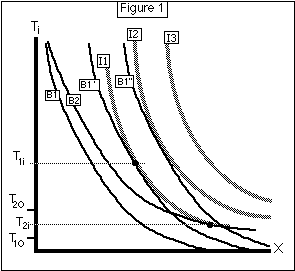
Proof: The solution is shown geometrically on Figure 1. B1, B1', B1'' are budget lines for T_o1; B2 is a budget line for T_o2. Since Z*, the optimal amount of insulation, is a function only of T_i-T_o, and C in equation 2'' depends only on Z* and T_i-T_o, the budget lines for any given value of To, such as B1, B1', and B1'', are identical except for a horizontal shift, and B2, corresponding to a different To, is equal to B1 shifted up by T_o2-T_o1.

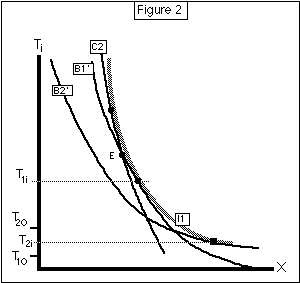
Figure 2 shows why a solution for which T_i2>T_i1 is impossible. C2 is a hypothetical budget line for T_o=T_o2 which is tangent to I1 at a temperature above T_i1. Since it cannot intersect I1, it must intersect B1', as shown. At point E, where they intersect, C2 crosses B1' from above, hence must be steeper than B1'.

But that is impossible. The slope of a budget line is the corresponding value of -1/P_t(Z*(T_i-T_o)). Z*(T) is a non-decreasing function of T by the lemma, and (T_E-T_o1)<(T_E-T_o2), so the slope of B1' at E must be at least as steep as the slope of C2. Hence Figure 2 is impossible. Hence we cannot have T_i2>T_i1. Hence T_i1<= T_i2. Q.E.D.

In drawing the figures, I have assumed that for a given set of values of W,r, and To there is only one Ti which maximizes U subject to the budget constraint. This need not be true, nor is it necessary for the proof. If there are multiple solutions, we simply apply the proof to the lowest value of T_i1 and the highest value of T_i2, demonstrating that the former is at least as high as the latter.

IV. Relaxing the Assumptions

Two assumptions made in the course of the argument can be relaxed without weakening the conclusion. The first is the assumption that of the three forms of heat transfer--conduction, convection, and radiation--only the first is significant. Heat loss from radiation is the difference between heat radiated away and heat absorbed. The former depends only on the temperature of the radiating object--in our case the interior of a house, radiating heat through the windows. The latter depends only on the temperature of the external objects whose radiation the house absorbs (and on characteristics of the house other than its temperature, such as its color). The formula for net heat flow by radiation is

H_r(T_i,T_o) = k(Ti⁴ - To⁴)

It follows that the increased loss through radiation as a result of an increase in T_i does not depend on T_o, which is all we need for the theorem to hold for radiation as well as for conduction.

The formula for heat loss by convection is

H(T_i,T_o) = K(T_i - T_o)^5/4

Hence the corresponding marginal cost goes as the one fourth power of the temperature difference; if convection is sufficiently important, houses in cold climates might be kept colder than houses in warm climates .⁶

I also assumed, in the course of the argument, that heat was available at constant cost. This is a reasonable assumption for inputs such as coal or fuel oil, although there are some exceptions for electricity. But heat is produced inside the house, and the production function need not be linear. It is hard to see any reason for diseconomies of scale, since one could always install two furnaces instead of one, but there might well be economies of scale. If so, the result would be to lower the marginal cost of T_i in colder climates, and so make the conclusion hold a fortiori .⁷

V. Thermal Shock

In the argument so far, I have ignored income effects by assuming that the inhabitants of Los Angeles and Chicago have not only the same utility functions but also the same utility. That seems, at first, implausible; inhabitants of Chicago, with their thermostats at 70 and the outside temperature at 0, have much higher heating bills, despite their better insulation, than inhabitants of Los Angeles with their thermostats at 65 and the thermometer at 60--and in addition, the inhabitants of Chicago must pay for the construction of well insulated houses. My justification for ignoring income effects is migratory equilibrium. The higher costs of living in Chicago must be balanced by lower property values, higher wages, or other benefits--that is why (some) people remain there when they could move to California.⁸

The conclusion that real incomes are equalized by migration breaks down in the case of an unexpected increase (or decrease) in fuel costs. The effect will be capitalized as a fall in the value of Chicago real estate and other immobile assets, but since these assets mostly belong to residents of Chicago the immediate effect will be to make Chicago residents poorer relative to residents of Los Angeles. If interior temperature is a normal good, its consumption will decrease. As those of us who lived in the cooler parts of the U.S. during the early seventies can testify, that is precisely what happened; when heating prices shot up, thermostats fell and remained low for several years. Whether long run migratory equilibrium, in incomes and interior temperature, has yet been restored is a question I leave to those who did not play a role in restoring it.

*: The opportunity to collect the data on which this article is based was due to the generosity of the Research School of Social Sciences, Australian National University and the Department of Economics, UCLA. I would also like to thank M. Friedman for helpful suggestions. An earlier sketch of the argument of this article appears in Chapter 21 of Friedman (1986).

REFERENCES

Bassett, C.R. and Pritchard, M.D.W., Environmental Physics: Heating, New York: American Elsevier Publishing Company, 1969.

Friedman, David, Price Theory: An Intermediate Text, Cincinnati: South-Western Publishing Company, 1986.

U.S. Department of Energy, Energy Information Administration, Residential Energy Consumpton Survey: Characteristics of the Housing Stock and Households 1978 , February 1980.

Footnotes

¹ The "amount" of heating is often given in degree days per year. This is legitimate only to the extent that my physical assumption holds. If heat flow is not linear in the difference between inside and outside temperature then heating cost is not a function of degree days; maintaining a temperature difference of twenty degrees for two days will require a different amount of heat than maintaining a temperature difference of forty degrees for the first day and zero for the second.

²This also explains why most of us keep the thermostat at the same temperature throughout the year, except when the outside temperature goes above our normal thermostat setting. The same intuition which suggests that houses should be colder in Chicago than in Los Angeles (because "it costs more to keep the house warm") also suggests that Chicago houses should be kept colder in January than in March. In both cases the argument confuses marginal and total cost.

³While I have concentrated on differences in insulation, exactly the same analysis applies to differences in the efficiency of heating systems or choice of fuel, since in each case the choice involves paying a higher fixed cost in order to have a lower marginal cost. Not surprisingly, the 1978 National Interim Energy Consumption Survey found that the percentage of households using electric heating (high marginal cost, low fixed cost) was highest in the South and West, and the percentage using fuel oil or kerosene was highest in the Northeast.

⁴If individuals never heat their houses, internal temperature is obviously higher in warmer climates. The complications of houses that are heated part of the year, so that T_i is constant during the heating season and equal to T_o otherwise, are assumed away to simplify the proof.

⁵More realistically, T_o could be included in the utility function and its direct effect on utility as well as its effect on heating cost compensated for by wage and/or rent differentials. One would then need the additional assumption that the tradeoff in the utility function between internal temperature and expenditure on other goods is unaffected by external temperature.

The overall effect would be to complicate the proof but to increase the size of the result. In colder climates individuals will have higher wages, above and beyond what is necessary to pay for the additional cost of insulation and heating, in order to compensate them for the disutility of being out in cold weather. A higher wage implies increased consumption of normal goods. If, as seems reasonable, internal temperature is a normal and not an inferior good, then houses in cold climates would be even warmer, relative to houses in warm climates, than my analysis indicates. The proof would fail, however, if for some reason internal temperature were an inferior good--perhaps because rich people liked to show off their fur coats by wearing them indoors.

⁶Throughout my discussion, I have spoken as though total heat loss were simply the sum of radiation, convection, and conduction losses. This is an oversimplification, since the transmission of heat may involve more than one of the processes. Consider an erg of heat which is conducted through insulation, convected across an air gap in the wall, then radiated away from the outside surface. Since the relevant marginal cost is independent of outside temperature for two of the processes and only weakly dependant for the third, the conclusion is unlikely to be altered save for very drafty houses.

⁷I have assumed throughout the discussion that fuel prices are the same in both warm and cold parts of the country. While this may not always be true, there seems no reason to expect them to vary systematically with climate.

⁸Some, but not all, readers may prefer to assume irrational behavior or imperfect information.

Back to the list of articles.

Back to my home page.