HANGED FOR A SHEEP-

THE ECONOMICS

OF MARGINAL DETERRENCE

Suppose the highest punishment imposed in a particular legal system is life imprisonment. Someone suggests that perpetrators of armed robbery, a particularly dangerous and unpleasant crime, deserve that punishment. From the standpoint of traditional legal scholarship, this proposal raises a variety of issues having to do with the justice of the punishment. From the standpoint of the economic analysis of law, it raises a much simpler question: Do we want to make it in the interest of armed robbers to kill their victims?

In thinking about an economically efficient set of criminal punishments, we usually start by considering a single crime and trying to find the optimal way of inducing potential offenders not to commit it.[2] This paper is concerned with a problem one step more complicated--the situation where a potential offender, if he commits an offense, will be choosing among two or more different crimes.[3] If he commits one crime he cannot (or, in more elaborate versions, is less likely to) commit the other. In such a situation, one of the considerations in setting punishments is the risk that a high punishment for one crime may shift the offender to committing a different, and perhaps a worse, one.[4]

This consideration arises in several different, and apparently unrelated, situations. The most obvious is summed up by the proverb quoted above. A thief has an opportunity to carry off one animal from the flock. If the penalty is the same whichever animal he chooses, he might as well take the most valuable: "As good be hanged for a sheep as a lamb." The same logic applies to more modern thefts. If we impose the same punishment however large the amount stolen, there is no incremental punishment for taking the VCR as well as the television.

A second situation is exemplified by the case of the robber killing his victim. Since the objective of the murder is to keep him from being caught for robbery, he has no interest in committing just murder; his alternatives are no crime, robbery, or robbery plus murder. This is similar to the previous situation if we thing of robbery as one crime and murder plus robbery as another.[5]

A third example is the distinction between robbery and armed robbery recognized in existing law. If we have already imposed the highest punishment we are willing to use for armed robbery, an increase in the punishment for ordinary robbery decreases the probability we will be robbed but increases the probability we will be robbed by someone carrying a gun. Some previously unarmed robbers will decide to quit the profession, but those who do not may find that the added security of carrying a gun is now worth the (lower) cost.

These examples can be generalized to a much wider range of situations. To the extent that different crimes are committed by people with the same special characteristics, such as a taste for risk, a deficient conscience, or skill in not being noticed, each of these crimes is a substitute for the others. A criminal who is mugging someone cannot be simultaneously burgling someone else's house. So our analysis will be relevant whenever the same sort of people commit several different sorts of crimes and choose among them in part on the basis of the expected cost of being caught and punished.

A fourth application is the distinction between punishing an attempt and punishing the completed crime.[6] In some cases, the difference between an attempt and a crime is merely chance. But in others, the attempt represents a crime abandoned when it became clear to the offender that it was more difficult, or more risky, than expected. One consideration in deciding whether to complete the crime will be the additional punishment for doing so.

In Part I, we analyze a situation with two alternative crimes; we assume that the cost function for apprehending offenders is the same for both. Part II generalizes the analysis of Part I to the case of more than two alternatives. In Part III, we consider the robber who may kill his victim in order to reduce the chance of being caught. In such a situation it is the cost function for catching the offender, rather than the benefit the offender receives from his offense, that depends on which crime he chooses to commit.

Part IV extends the analysis to situations where different crimes are substitutes but not strict alternatives. In Part V, we consider how our conclusions are affected by varying our assumptions about the cost function for catching and punishing criminals. Part VI discusses the relation between the predicted pattern of effective punishment and the predicted pattern of actual punishment, and compares our results to others in the recent literature.

Throughout the discussion, we attempt both to describe a formal solution to the problem of optimal punishment and to answer two questions about that solution. The first question is how optimal punishment varies with the damage done: ought the more serious crime always be punished more severely? The second is how the possibility of one crime affects the optimal punishment for another: does the presence of sheep that a thief might steal increase or decrease the optimal punishment for stealing a lamb?

I. Only Two Alternative Crimes

A potential offender can choose to commit no offense, to steal a lamb, or to steal a sheep. Benefits are defined relative to committing no offense. The benefit to the offender is B_L for lamb theft, B_S for sheep theft. A population of potential offenders can be characterized by a probability distribution [[rho]](B_L,B_S). We assume that the loss of a lamb costs the shepherd a fixed amount of damage D_L per offense and the loss of a sheep costs a fixed amount D_S>D_L per offense.

We deter commission of a crime by imposing a punishment (P) with a probability (p). The cost of catching a fraction p of the offenders is an increasing function of p, number of offenses held constant; it costs more to catch 10 criminals out of 100 than to catch 5. The cost per offense of punishing offenses, measured as a percentage of the amount of punishment, increases with the size of the punishment.[7]

The first step in constructing an optimal system is to find the least expensive way of imposing a given amount of deterrence. Consider all of the probability punishment pairs (p_i,P_i) that are equivalent to each other from the standpoint of the criminal and thus have the same deterrent effect.[8] Pick the one for which the sum of apprehension cost and punishment cost is lowest. Repeat for every level of deterrence. You now have a cost curve for deterrence, showing the cost of imposing any level of deterrence via the least costly combination of probability and punishment. We call the certainty equivalent of a punishment/probability pair the effective punishment[9] and the per offender cost of imposing it--apprehension plus punishment--the enforcement cost.

Increasing the effective punishment requires an increase in probability, punishment, or both. Since cost rises with either probability or punishment, higher levels of deterrence cost more per offense.[10] We assume that apprehension and punishment costs do not depend on the crime--it is as easy to catch a robber who steals a lamb as one who steals a sheep. C(F) is the cost of imposing on the offender a combination of punishment and probability equivalent to a certain fine of F.

We assume that there is some limit to the ability of the enforcement system to deter, some F^max such that no feasible punishment/probability pair has a certainty equivalent greater than F^max. As F approaches F^max, enforcement cost approaches infinity. We also assume that there are some offenders whose benefit from committing at least one of the crimes is greater than F^max. Without those assumptions, our model leads to a simple, implausible, and uninteresting solution in any situation where all offenses are inefficient:[11] impose effective punishments that deter all offenses. Since no offenses occur there is no damage, hence no damage cost, no punishments to be imposed, hence no punishment cost, and no criminals to be caught, hence no apprehension or conviction cost.[12]

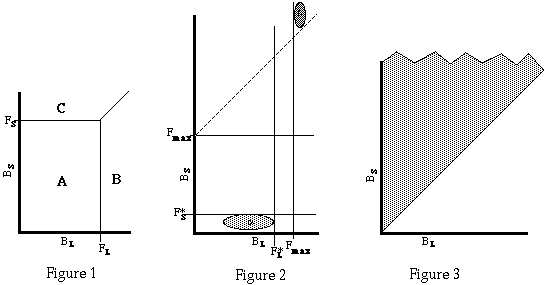
Figure 1 shows the positive quadrant of a plane whose dimensions are B_L and B_S. F_L is the effective punishment for stealing a lamb, F_S for a sheep. An offender who chooses to steal a sheep receives a benefit of B_S at a cost of F_S, so his net benefit is B_S-F_S, and similarly for an offender who chooses to steal a lamb.

Region A contains values of B_L and B_S such that a potential offender will choose not to commit either crime. Region B contains values for which a potential offender will maximize his net benefit by stealing a lamb. Region C contains values for which a potential offender maximizes his net benefit by stealing a sheep. To find total costs and benefits for this particular pair of effective punishments, we integrate over each region the costs and benefits from the action taken by offenders in that region weighted by the density of offenders [[rho]](B_L,B_S). We have:

Net Cost=Damage Cost + Enforcement Cost - Benefit to Offenders

NC= + (Equation 1)

If we had explicit functions for C(F), [[rho]](B_L,B_S), D_S and D_L, we could set

and solve the two equations for the optimal pair of effective punishments (F_S*, F_L*).

---

---

Query: Can we prove that the optimal effective punishment for the more serious offense is at least as great as for the less serious?

Without additional assumptions, the answer is no. Consider Figure 2. Suppose that regions [[alpha]] and [[beta]] contain almost all potential offenders, with many more in [[alpha]] than in [[beta]]. By setting F_L* and F_S* as shown, we deter everyone in [[alpha]]. Potential offenders in [[beta]] cannot be deterred by any punishment we can impose. We minimize the cost of punishing them by choosing the lowest level of punishment sufficient to deter those in [[alpha]].[13] By making the ratio of offenders in [[alpha]] to offenders in [[beta]] sufficiently high, we can guarantee that deterring the former is worth the cost of punishing the latter.

Is it possible to improve on this result by making the additional punishment for sheep theft high enough so that potential offenders in [[beta]] will at least limit themselves to stealing lambs? No. The highest possible marginal punishment for stealing a sheep instead of a lamb is achieved by setting F_L=0, F_S=F^max. The dashed diagonal line divides the regions that then correspond to B and C on Figure 2. Region [[beta]] lies above the line, so even with the highest possible difference between the two punishments, offenders in that region will still steal sheep. We might think of the offenders in region [[alpha]] as gourmets who strongly prefer the flavor of lamb to that of sheep. Those in region [[beta]] are simply very hungry--and sheep are bigger than lambs.

Suppose we add an additional assumption: that the crime which imposes larger costs on the victim also provides larger benefits for the criminal, so that offenders always prefer, at equal punishments, to commit the more serious crime.[14] Figure 3 shows that situation; [[rho]](B_L,B_S) is zero whenever B_L>=B_S. Offenders only exist in the shaded region of the figure. In this situation, we have:

Theorem: There exists a pair of punishments (F_L, F_S*) such that F_L*<= F_S* and net cost is at least as low as for any pair of punishments for which that is not true.  

Proof: For any given level of F_S, all levels of F_L>=F_S produce the same result: Nobody steals lambs, the punishment F_L is never applied, and whether someone steals a sheep depends only on F_S. It follows that, for any given level of F_S, the net cost with F_L=F_S is the same as for any F_L>F_S. If a lowest cost pair has F_L<=F_S, then our theorem holds. If a lowest cost pair has F_L>F_S, then there is another pair with the same value of F_S and with F_L=F_S which satisfies the theorem.  [15]  QED

The argument so far has assumed a continuous density of offenders. With a finite number of offenders, we can prove a stronger result.

Theorem: Assume a finite number of offenders; for each offender i , B_Lⁱ<B_Sⁱ. Then there exists a pair of punishments (F_L*, F_S*) such that F_L*<F_S* and net cost is at least as low as for any pair of punishments for which that is not true.  

If, for any optimal pair of punishments, at least one offender commits the lesser crime, and if C(F) is a strictly increasing function of F, then we may replace "at least as low as" with "lower than" in the conclusion of the theorem.  

Proof: Assume the contrary; there exists some pair (F_L**, F_S**) for which F_L**>= F_S** and net cost is lower than for any pair (F_L, F_S) such that F_L< F_S.  

Let [[Delta]] be the smallest value of (B_Sⁱ-B_Lⁱ) for any offender i. By our assumption, [[Delta]]>0  

Set F_L*= F_S**-[[Delta]]/2.  

Set F_S*=F_L**.  

We now have a pair (F_L*, F_S*) such that F_L*< F_S*. The same offenses occur with (F_L*, F_S*) as with (F_L**, F_S**), so damage to victims and benefit to offenders are the same. The level of effective punishment is the same for one crime and lower for the other, so enforcement costs are either the same or lower.  

If the optimum has at least one offender stealing a lamb, and if C(F) is strictly increasing in F, then enforcement cost is less for (F_L*, F_S*) than for (F_L**, F_S**) since F_L* is lower , and therefore less costly to impose, than F_L** .  QED

Query: Can we prove that the optimal punishment for the more serious crime is larger than if the lesser crime did not exist--that the optimal punishment for stealing a sheep is larger than if there were no lambs?  

Answer: No--it is not true. The same answer holds if we reverse the question and ask whether the optimal punishment for stealing a lamb is lower than if there were no sheep.

We might expect that eliminating sheep from the flock would permit a higher punishment for stealing a lamb, since we would no longer have to worry that doing so would cause thieves to steal sheep instead. The reason this is not always true has to do with punishment costs. Consider a thief who values both sheep and lambs very highly--so highly that, if there are sheep in the flock, no feasible punishment/probability combination will deter him from stealing a sheep, and if there are only lambs in the flock no combination will keep him from stealing a lamb. Further suppose that he much prefers stealing sheep; if both are available he will choose to steal a sheep, whatever the punishments and probabilities.

If there are both lambs and sheep in the flock, the existence of such a thief affects the optimal punishment for stealing a sheep. He cannot be deterred but he can be punished, and the cost of doing so is one of the arguments against raising the punishment for stealing sheep. It is not, however, an argument for or against raising the punishment for stealing a lamb. As long as there are sheep available, the punishment for lamb stealing will neither deter him (since he prefers to steal a sheep anyway) nor have to be imposed on him.

Now suppose the sheep all die; we have only lambs in the flock. The existence of this thief suddenly becomes a reason to lower the punishment for stealing a lamb. With no sheep available he is going to steal a lamb, whatever we do, and the higher the punishment for doing so the larger the cost of punishing him. If enough thieves are of this sort, the optimal punishment for stealing lambs will be lower when there are no sheep in the flock.

For a geometric version of the argument, consider Figure 2 again. The thief described above is in region [[beta]]. The more thieves are in region [[beta]], the lower the optimal punishment for stealing a lamb-provided there are no sheep for them to steal instead.

II. Multiple Alternative Crimes

So far we have assumed that there are only two alternative crimes; we now drop that assumption. We continue to assume that the different crimes are alternatives: an offender has the opportunity to commit only one offense.

In the previous section, we showed how we could derive two equations from which the optimal pair of effective punishments could be calculated. Repeating the analysis for N potential crimes would yield N similar equations in N variables. These equations describe an optimum in which slightly increasing any one punishment produces a gain from offenders substituting to less damaging crimes (including no offense) that just balances the loss from offenders substituting to more damaging crimes plus the increase (or minus the decrease) in enforcement cost.

In Part I we showed that, without additional assumptions, the effective punishment for the more serious crime might be lower than for the less serious. Since the situation analyzed there was a special case of the situation analyzed here, that negative result still applies. Can we also generalize our positive result?

Query  : Can one prove that, if benefit to offender has the same ordering as damage to victim, then optimal punishment also has the same ordering?  

Answer:   Yes

We define:

D_i: damage done by crime i

F_i: Effective Penalty for crime i

: Benefit potential offender k will receive if he commits crime i.

We assume a finite number of potential offenders. We also assume:

If i>j, then D_i>D_j (Condition 1)

If i>j, then > for all potential offenders k (Condition 2)

for i>j, let [[Delta]]_ij be the smallest value of - for any offender k.

It follows that there exist some set of effective punishments {F} such that

If i>j, then F_i>F_j (Condition 3)

and the net cost of crime with {F} is at least as low as under any alternative set of punishments.

Proof: Suppose the contrary. Then there exists a set of punishments {F**} for which net cost of crime is lower than for any {F} satisfying condition 3. Since {F**} does not satisfy the condition, there must be some pair i,j such that

i>j and F_i**<=F_j** (Condition 4)

From condition 2, we know that > for all potential offenders k, hence ( -F_i**) > ( -F_j**) for all potential offenders k. Every offender is better off committing crime i than committing crime j, so nobody commits crime j.

Now replace {F_i**} with {F_i*}, where the only change between the two sets of punishments is that F_j*=F_i**- [[Delta]]_ij. The net benefit of committing crime j is still less than the net benefit from committing crime i. Repeat this for every pair i,j satisfying condition 4. We end up with a set of penalties that produces at least as good a result as {F**} and satisfies condition 3. So the assumption that no such set exists leads to a contradiction. QED

III. The Choice Between Robbery and Robbery plus Murder

We now return to the case of the robber deciding whether to kill his victim. His objective in doing so is not a larger benefit but a lower probability of being caught. We have:

For all i, B_rⁱ=B_rmⁱ: The benefit to any criminal of robbery and of robbery plus murder are the same.

D_r<D_rm: Robbery plus murder imposes a larger cost on the victim than robbery alone.

For all F>0, C_r(F)<C_rm(F): It is harder to catch robbers who kill their victim, so the cost of imposing any level of effective punishment on them is higher.

It follows that F_r^max>=F_rm^max: The highest effective punishment that it is possible to impose for robbery is at least as high as for robbery plus murder.

Our tie breaking rule is that the offender commits the lesser crime if net benefit to him is the same for both.

Given these assumptions, the optimal pattern of effective punishment must have F_r <= F_rm. To see why, suppose the contrary; let the optimal effective punishments be (F_r*, F_rm*), F_r*> F_rm*. Consider as an alternative the pair (F_rm*, F_rm*). The number of offenses remains the same, but all offenders switch from robbery plus murder to simple robbery. The benefit to the offenders is the same, the cost to the victims is less, and the cost to the enforcement system is less, since we are imposing the same expected punishment (F_rm*) on the same number of offenders as before, and it is cheaper to impose a given expected punishment on an offender who has not killed his victim: C_r(F_rm*)<C_rm(F_rm*). (F_rm*, F_rm*) is a superior set of punishments to (F_r*, F_rm*), so the former cannot have been, as we assumed, the optimal set. It follows that, for the optimal set, F_r <=F_rm. [16]

Increasing the punishment for robbery plus murder above the punishment for robbery has no effect on either the number of offenses (there are no murders to be deterred) or the cost of enforcement (there are no murderers to be caught and punished); for simplicity, we set the two effective punishments equal. If we were taking account of complications such as imperfect information and criminals who differed in how easy they were to catch, we would want to make the effective penalty faced by the average offender for murder plus robbery significantly higher than for robbery alone,[17] in order to deter atypical robbers from killing their victims.

To choose the level of effective punishment, we find the value of F_r that minimizes net cost, subject to the condition that F_r=F_rm<F_rm^max. Since nobody is committing robbery plus murder, the relevant costs are all for simple robbery, and the calculation is the same as if murder were not possible, except that in that case the constraint would be F_r<F_r^max. If that constraint is not binding--if we do not have a corner solution at F_rm^max--the optimal punishment for robbery is the same whether or not murder is an option. If the constraint is binding, then the possibility of murder lowers the optimal punishment for robbery.

IV. Different Crimes as Substitutes for Each Other

So far, we have considered offenders who choose one out of a set of alternative crimes-although we have allowed one crime to be a combination such as robbery plus murder. While this may describe the situation of a robber deciding whether or not to murder his victim, it seems less appropriate for a thief who may choose to steal a lamb today and a sheep tomorrow, and still less for a criminal with a mixed career in burglary, robbery, and extortion.

One possibility for analyzing such situations would be to treat each possible combination of crimes as a different crime; the offender would be choosing (and being punished for) a particular criminal career. In practice, courts rarely have complete information about the careers of the criminals they punish. They do, however, have some information, and can and do use it to make the punishment of one offense depend to some degree on what other offenses the criminal has committed.

An alternative approach is to consider different crimes as substitutes rather than alternatives. If two goods are substitutes, an increase in the price of one--in this case, the effective punishment for one crime--increases the demand for the other. This is a more general approach to marginal deterrence than our earlier assumption that crimes are alternatives, substituting for each other on a strict one for one basis.

Why might we expect different crimes to be substitutes for each other? An offender owns inputs, such as his own labor, used in the production of offenses. Time spent committing one crime increases his income and reduces his leisure, making the commission of other crimes less attractive. If the punishment for one crime increases, some offenders will choose not to commit it, making them more willing to commit other crimes. If we raise the punishment for robbery while leaving the punishment for burglary unchanged, we expect an increase in the number of burglaries.

In earlier sections, we considered two questions: "will the more serious crime have a higher effective punishment?" and "what effect does the possibility of one crime have on the optimal punishment for the other?" The arguments made there can be restated here in a more general form.

We minimize the cost associated with a crime by setting effective punishment at the level at which the benefit of raising it a little farther would be just balanced by the cost. The benefit is due to the reduction in the number of offenses as a result of the increase, and so depends on the slope of the demand curve. The cost is the cost of imposing a more severe effective punishment on those not deterred, which depends on how many of them there are--the quantity demanded.[18] So the optimal effective punishment depends on the shape of the demand curve, which determines the relation between level of demand (quantity demanded at a price) and slope (how fast the quantity demanded changes with changes in price). The assumption that two crimes are substitutes tells us how the demand for one changes when the price of the other is changed but it does not give us a relation between the shapes of the two curves, so it does not tell us which crime should have the higher effective punishment.

Can we predict how the optimal effective punishment for one crime will depend on the possibility of the other? Figure 4a shows two demand curves for stealing lambs. Each shows quantity stolen as a function of the price-the effective punishment. D_LS is the demand curve if both lambs and sheep are available to be stolen, D_L the demand curve if there are only lambs. D_L is to the right of D_LS because the two crimes are substitutes; eliminating one is equivalent to raising its price to infinity, and so increases demand for the other.

In setting an optimal level of effective punishment, we are trading off the benefit of deterring additional offenses against the cost of punishing those offenses we do not deter. At any particular level of effective punishment, such as F^o on Figure 4a, the cost of slightly increasing the punishment is proportional to the number of offenses occurring--the quantity demanded at that price. The benefit is proportional to the inverse slope of the demand curve--the rate at which number of offenses decreases as effective punishment increases. The benefit also depends on whether deterring a thief from stealing a lamb means that he steals nothing or steals a sheep instead.

---

---

In Figure 4a, D_L is twice D_LS; at any level of effective punishment, twice as many lambs are stolen if there are no sheep in the flock to steal instead. In that situation, the slope of D and the quantity demanded at any price increase by the same factor, leaving the balance between cost and benefit unchanged. If that were the only effect of eliminating sheep from the flock, the optimal punishment would be the same before and after the change.

But it is not the only effect. Eliminating sheep also increases the benefit associated with deterring thieves from stealing lambs, since it eliminates the problem of deterring them into stealing sheep instead. So if, at some optimal effective punishment F_LS*, the benefit from further increasing the punishment for stealing a lamb just balanced the cost when both sheep and lambs were in the flock, then eliminating the sheep while keeping the effective punishment for stealing lambs the same would make the benefit of increasing the effective punishment larger than the cost, so the optimal effective punishment in that situation, F_L*, would be greater than F_LS*.

All of this depends on the assumption, implicit in Figure 4a, that the slope and the value of D changed by the same factor when we shifted from D_LS to D_L. If the inverse of the slope of D at F_LS* increased by a larger factor than the value of D, as it does at F^o on Figure 4b, the argument holds a fortiori.

But if the inverse slope increases less than the value, as on Figure 4c, the argument no longer holds. In that situation, the elimination of sheep from the flock increases the number of thieves who must be punished for stealing lambs (at a given level of effective punishment F_LS*) by more than it increases the number who will be deterred by a small increase in the effective punishment. If that effect is strong enough, it can outweigh the increase in the benefit from deterring thieves due to the elimination of sheep that the thieves might steal instead. We then end up with F_L* less than F_LS*. Without some further assumption about how the slope of the demand curve for the one crime changes with the price of the other, we cannot show that the possibility of the more serious crime necessarily lowers the optimal punishment for the less serious.

Two effects are associated with the elimination of sheep from the flock. One, the increased benefit of deterrence, moves the optimal punishment for stealing lambs in an unambiguous direction--up. The other, the possible change in the ratio between the slope and the value of demand, could go either way. With one effect that increases the optimal punishment and another that might equally well increase it or decrease it, we may perhaps say that we have a weak presumption for a net increase.

V. Different Cost Functions

Throughout this paper, we have assumed that the cost of imposing a given probability of apprehension is proportional to the number of offenders-that it costs twice as much to apprehend twenty offenders out of two hundred as it does to apprehend ten out of a hundred. Steven Shavell, in his recent paper on marginal deterrence,[19] makes a very different assumption. His cost function is independent of the number of offenses. It costs more to apprehend twenty criminals out of a hundred than ten out of a hundred, but it costs the same amount to apprehend twenty out of a hundred as two hundred out of a thousand.

While one can imagine a technology of apprehension with these characteristics--cameras on every street corner, perhaps, taking photographs at random intervals--it seems implausible. It would not be surprising, however, to find less extreme economies (or diseconomies) of scale in the production function for apprehensions. It is therefore worth asking how our results would be affected if we generalized our cost function. Instead of assuming that:

TC(F,O)=O x C(F)

where TC(F) is the total cost of imposing an expected punishment of F on each of O offenders, and C(F), as before, is the cost per offender of imposing an expected punishment of F, we write:

TC(F,O): >=0 ; >= 0

What can we say about the effect of this generalization of the cost function on our results?

Our negative results are unaffected. The model we have been using is a special case of the more general model, so a counterexample under the former is a counterexample under the latter as well. There remains the question of which of our positive results hold in the more general case.

Consider the case of the robber who might kill. One element in our argument was that, by keeping the effective punishment for that crime above the effective punishment for simple robbery, we could reduce the number of such killings to zero, saving both the lives of the victims and the extra cost of catching (or punishing more severely) robbers who had eliminated the witnesses to their offenses. If enforcement cost does not go to zero with the number of offenses, things are not quite so simple.

Our conclusion, however, still stands.[20] Any schedule of punishments in which the effective punishment is lower for the robber who kills his victim is dominated by one with the same effective punishment for that case and with the effective punishment for robbers who do not kill their victims lowered to the point where the robbers just find it in their interest to switch to the less violent strategy. The only change is that, instead of concluding that the effective punishment for the robber who kills his victim should be at least as great as for the robber who does not, we now conclude that the two should be equal,[21] since an increase in the effective punishment for the more serious crime above that necessary to deter it may be costly even if no offenses occur.

Our other conclusion was that the optimal punishment for robbery was unaffected by the possibility that the robber might kill his victim, except in the case of a corner solution, where the optimal effective punishment for robbery alone was above the maximum feasible punishment for a robber who killed his victim. That conclusion no longer holds under the more general cost function. The cost of any level of effective punishment for robbery now includes the standby cost necessary to impose that same effective punishment on the (more difficult to apprehend) crime of robbery plus murder. So the marginal cost of increasing the effective punishment for robbery is higher if it is possible for robbers to kill their victims, leading to a lower optimal effective punishment.

The other positive result we got was that punishment should increase with severity in the models of Parts I and II, provided that the more serious crime also provided a larger benefit to the offender, as in the case of stealing more or more valuable objects. The proof of that result did not depend on the details of the cost function, so it still holds.

VI. Punishment and Effective Punishment

In analyzing the implications of marginal deterrence for optimal punishment, we have concentrated on questions involving the effective punishment for a crime--the certainty equivalent of the combination of probability and actual punishment imposed on those who commit it. Previous authors[22] have asked our first question with regard to actual rather than effective punishment: Is the optimal actual punishment higher for the more severe of two alternative crimes? What can we say about the relation between that question and the one we have been answering; if the effective punishment for one crime is higher than for another does that imply that the actual punishment is also higher?

In the most general case, the answer is no. In picking a particular combination of probability and punishment, we look for one that provides a given effective punishment at the lowest cost. If the cost functions for catching offenders are different for different crimes, then the efficient probability/punishment combinations will be different as well. If, for example, the more serious crime happened to be much easier to detect, we might want to punish it with a high probability of a moderate punishment, while punishing the less serious crime with a much lower probability of a somewhat higher punishment. The result would be a higher effective punishment for the more serious crime but a lower actual punishment.

This is a pattern that we sometimes observe. Double parking in a busy street probably does more damage than throwing a paper napkin out of a car window-but the fine for littering may well be higher than the fine for double parking, reflecting the fact that only a very small fraction of litterers are caught. We do not know of any similar cases involving crimes that, like those we have been discussing, are alternatives or substitutes. We can, however, suggest a hypothetical one:

A town bans the burning of leaves. Homeowners face three alternatives. They can pay to have their leaves hauled away. They can burn them and risk a fine. Or they can put their leaves in trash bags and dump the bags on someone else's property when nobody is watching. Burning the leaves does the most damage, but is much easier to detect than dumping. The optimal pattern of punishments will probably impose a higher expected punishment for burning but a higher actual punishment for dumping.

As this example suggests, the result which previous authors have looked for--higher optimal punishments for more serious offenses--cannot in general be established because it is not in general true. In order to get it, we require additional assumptions. The main one is that the cost function for catching and convicting offenders is the same for all of the alternative offenses being considered. In addition, we assume increasing marginal cost for both catching and punishing criminals. These latter assumptions imply that the least costly way of increasing effective punishment is by increasing both probability and punishment. It follows that, if the more serious crime has the higher effective punishment, it will also have the higher actual punishment.

The difference between our emphasis on effective punishment and the emphasis in the previous literature on actual punishment is both a cause and a consequence of important differences in assumptions. In Shavell,[23] punishment cost is assumed to be zero; in Wilde[24] and in Reinganum and Wilde[25] it is proportional to the size of the punishment. Under either set of assumptions, a situation where punishment is below its maximum feasible level can always be improved by raising the punishment and lowering the probability of inflicting it, keeping expected punishment constant. It follows that the optimal punishment for a single offense is always the highest feasible. With multiple offenses, one would expect marginal deterrence to be provided by imposing the same (maximal) punishment on all offenses and varying the enforcement effort so as to catch a smaller fraction of offenders for less serious offenses.

In order to avoid this result,[26] all three papers assume that apprehension for different offenses is a joint product of a single enforcement effort. The probabilities of apprehension for two alternative offenses are determined by the same decision, so the only way of changing the expected punishment for one without changing the expected punishment for the other is by altering the punishment. One offense receives the maximal punishment, the other a lower punishment. Additional assumptions are needed to make sure that it is the more serious offense that receives the higher punishment.

These papers thus introduce an artificial assumption about enforcement costs in order to eliminate a problem created by an artifical assumption about punishment costs. The problem does not arise with our more realistic model. Once you allow the ratio of punishment cost to punishment to increase with the size of the punishment, problems associated with always imposing the highest feasible punishment disappear, since even if there is a highest feasible punishment there is no reason to expect it to be optimal.

In addition to avoiding some of the artificial assumptions of the earlier papers,[27] we also generalize the analysis to a wider range of problems--more than two crimes and crimes that are substitutes but not alternatives.[28] In addition to the question of relative punishments, we also consider the effect of the possibility of one crime on the punishment for the other. And we discuss explicitly, in Part V, the effect of differing assumptions about the form of the cost function for catching and punishing offenders.

VII. Conclusion

We have been analyzing optimal punishment in situations in which one crime is a substitute for another. The obvious intuition is that we should keep the punishment for the less serious crime down so as not to tempt offenders to switch to the more serious. It is that intuition, seen from the standpoint of the thief rather than the law maker, that is behind the proverb with which we started our discussion.

The economics are less clear than the intuition. The benefit of deterring a thief from stealing a lamb is less when the result may be that he steals a sheep instead, which is an argument for a lower punishment. But the existence of sheep to be stolen may, by reducing the number of thieves who steal lambs, reduce the cost of catching and punishing them, which lowers the cost of imposing any particular level of effective punishment and raises the optimal punishment. When we add in the distinction between the number of thieves on the margin and in total and note that including sheep in the flock may affect the two numbers in different ways, the situation becomes complicated enough to make a purely verbal analysis difficult. The result of a more formal treatment turns out to be ambiguous. While there is some presumption that the possibility of the more serious crime will lower the optimal penalty for the less serious, the opposite effect is possible.

Whether the more serious crime should have the more severe effective punishment is also less clear in the analysis than in the intuition. The answer is "yes" if the offender's only objective in committing the more serious crime is to make it harder to catch him. It is also "yes" if crimes are alternatives and the benefit to the criminal is always larger for the more serious crime. Thus our analysis does imply that a thief should be punished more severely the greater the value of what he chooses to steal-that there should be some incremental punishment for taking the VCR as well as the television.[29]

Our analysis does not, however, imply that punishment should rise with severity in the general case. Where a criminal is choosing between two alternative crimes but where some criminals may prefer (punishment aside) the less serious of the two, the optimal schedule of punishments might punish the less serious crime more severely, as we showed in Part I. Where two crimes are substitutes but not alternatives, there is no necessary relation between their punishments. And even if effective punishment does increase with severity, that implies that actual punishment increases with severity only if the difficulty of catching an offender is independent of his offense.