Reprinted from THE BELL JOURNAL OF ECONOMICS Vol. 10, NO. 2, Autumn 1979 Copyright 1979, American Telephone and Telegraph Company
David D. Friedman*
Discriminatory pricing by railroads may be better than marginal cost pricing with a subsidy of the resulting losses, since it gives the railroad correct incentives for deciding what rail lines to build. The argument, applied to long- haul/short-haul discrimination, shows that its prohibition may lead to non- optimal construction decisions.
One of the most notorious "abuses" of the nineteenth century railroad industry was the long-haul/short-haul discrimination, the practice of charging higher rates for shipping freight (or passengers) between two intermediate points on a line than for shipping the same cargo the full length of the line, including the intermediate section. At first glance, this seems as unreasonable a policy as it would be to charge more for a one-pound package of cornflakes than for a two-pound package. I shall show that the price structure involved actually generates an efficient set of incentives (for railroads) and that a prohibition of long-haul/short-haul discrimination, such as Section 4 of the 1887 Act establishing the ICC, would produce undesirable consequences.[1] I shall assume, except where the contrary is explicitly stated, that railroads are capable of perfect discriminatory pricing. This assumption, while an approximation, is not an unreasonable one, considering the complexity of rate schedules, both in the nineteenth century and today, designed precisely for that purpose.[2]
It is generally agreed that the long-haul/short-haul discrimination resulted from situations where railroads had a monopoly on the short haul but were forced to compete on the long haul. Consider first the case of a railroad running from point A to point C via B, and facing competition from a perfectly competitive shipping industry which ships goods between A and C with marginal cost (equal to average cost equal to price) of Po (Figure 1). Assume for simplicity that the railroad's cost structure consists of a sunk cost CAC = CAB + CBC (the sunk cost of a line from A to C is the sum of costs from A to B and from B to C) plus a constant variable cost VAC = VAB + VBC (similarly). Let DAC be the total demand for transport from A to C, DAB, DBC (similarly). Assume that the transport services provided by rail and by water are identical.
The railroad will maximize its profit by charging (discriminatory) price schedules for transport from A to B and from B to C which exactly follow DAB and DBC down to the point where they cross VAB and VBC (see Figure 2). It will charge a similar schedule for transport from A to C, but because of the competition of water transport that will mean a fixed price of P, for all customers who would otherwise ship by water, and a discriminatory price schedule running from Po down to VAC to capture the right-hand tail of the demand schedule (see Figure 2). If Po is lower than the highest portion of either DAB or DBC, this set of price schedules is characterized by long-haul/short-haul discrimination--for some classes of goods, the price for the long haul is lower than for the short haul.
Let us now consider a firm deciding whether to build a rail line such as that shown in Figure I. The return it can expect is the sum of the total value (to the customers) of the services it produces on the segments AB, BC, and AC. In the first two cases this value is the area under the demand curve; in the third it is the area under the demand curve for rail transport, given the existence of water transport. This is precisely the social value of building and operating such a line.[3] It will build the line if and only if that value is enough to pay for the actual costs, fixed plus variable. It will make similar calculations for the segments AB and BC separately to decide whether to build the entire line or only part of it. If the railroad were forbidden to charge a higher price for the short haul than for the long, it would either have to give up some of the business it might have carried on the long haul, or fail to capture some of the consumer surplus it generates on the short haul; in either case its incentives would be distorted in such a way as to discourage the building of some desirable lines.
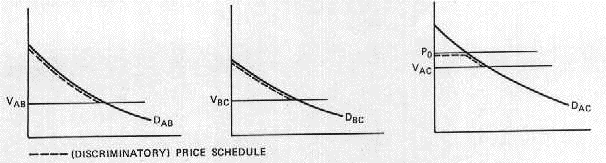FIGURE 2 PROFIT MAXIMIZATION
Coase, R.H. "The Marginal Cost Controversy." Economica, Vol. 13 (1946), pp. 169-182.
Hadley, A.T. Railroad Transportation. New York: Putnam, 1885.
Hille, S.J. AND Post, R.F. Jr., EDS. Transportation: Principles and Perspectives. Danville, N.J.: Interstate, 1974.
Kolko, G. Railroads and Regulation. New York: Norton, 1965.
Locklin, D.P. "The Literature on Railway Rate Theory." Quarterly Journal of Economics, Vol. 47 (1933), pp. 167-230.
Pigou, A.C. The Economics of Welfare. London: MacMillan, 1950.
[1] The observation that under certain circumstances the prohibition of long-haul/short-haul discrimination would make it unprofitable to build a line at all was made by Hadley (1885, pp. 114-115) and commented on by Pigou (1950). The general argument for the superiority of discriminatory pricing to marginal cost pricing is in Cease (1946), in the form of an argument for multipart pricing. The article contains references to earlier statements of the argument.
[2] Explicit price discrimination, under the euphemism of "value of service" pricing, has been common practice among railroads for at least a hundred years; it frequently goes so far as to discriminate between identical items of freight intended for different uses. During the 19th century, price discrimination among different shippers of the same commodity based on differing elasticities of demand for rail service was accomplished by individually bargained reductions in freight rates--the notorious "rebates." There were about 6000 items in the freight classification used in one region of the country in 1909 (Kolko, 1965, p. 170). See also Hille and Foist (1974, p. 183).
[3] Note that since water transport is perfectly competitive and uses factors that are, in the long run at least, available at constant cost, no producer surplus is lost by its elimination. *Assistant Professor, Virginia Polytechnic Institute and State University.