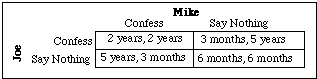
Table 8-1
"There are two kinds of people in the world: Johnny Von Neumann and the rest of us."Attributed to Eugene Wigner, a Nobel Prize-winning physicist
Economics assumes that individuals rationally pursue their own objectives. There are two quite different contexts in which they may do so, one of which turns out to be much easier to analyze than the other. The easy context is the one where, in deciding what to do, I can safely treat the rest of the world as things rather than people. The hard context is the one where I have to take full account of the fact that other people out there are seeking their objectives, and that they know that I am seeking my objectives and take account of it in their action, and they know that I know ... and I know that they know that I know ... and .... .
A simple example of the easy kind of problem is figuring out the shortest route home from my office. The relevant factors—roads, bridges, paths, gates—can be trusted to behave in a predictable fashion, unaffected by what I do. My problem is to figure out, given what they are, what I should do.
It is still the easy kind of problem if I am looking for the shortest distance in time rather than in space and must include in my analysis the other automobiles on the road. As it happens, those automobiles have people driving them, and for some purposes that fact is important. But I don't have to take much account of the rational behavior of those people, given that I know its consequence—lots of cars at 4:30 P.M., many fewer at 2 P.M.—by direct observation. I can do my analysis as if the cars were robots running on a familiar program.
For a simple example of the harder kind of problem, assume I am in a car headed for an intersection with no stop light or stop sign and someone else is in a car on the cross-street, about the same distance from the intersection. If he is going to slow down and let me cross first, I should speed up, thus decreasing the chance of a collision; if he is going to try to make it through the intersection first, I should slow down. He faces the same problem, with roles reversed. We may end up both going fast and running into each other, or both going slower and slower until we come to a stop at the intersection, each politely waiting for the other.
To make the problem more interesting and the behavior more strategic, assume that both I and the other driver are male teenagers. Each of us puts what others might regard as an unreasonably low value on his own life and an unreasonably high value on proving that he is courageous, resolute, and unwilling to be pushed around. We are playing a variant of the ancient game of "Chicken," a game popular with adolescent males and great statesmen. Whoever backs down, slows enough so that the other can get through the intersection, loses.
If I am sure he is not going to slow down, it is in my interest to do so, since even an adolescent male would rather lose one game of Chicken than wreck his car and possibly lose his life. If he knows I am going to slow down, it is in his interest to speed up. Precisely the same analysis applies to him: If he expects me to go fast, he should slow down, and if he is going to slow down, I should speed up.
This is strategic behavior, behavior in which each person's actions are conditioned on what he expects the other person's actions to be. The branch of mathematics that deals with such problems, invented by John von Neumann almost sixty years ago, is called game theory. His objective was a mathematical theory that would describe what choices a rational player would make and what the outcome would be, given the rules of any particular game. His purpose was to better understand not merely games in the conventional sense but economics, diplomacy, political science—every form of human interaction that involves strategic behavior.
It turned out that solving the general problem was extraordinarily difficult, so difficult that we are still working on it. Von Neumann produced a solution for the special case of two-person fixed-sum games, games such as chess, where anything that benefits one party hurts the other. But for games such as Chicken, in which some outcomes (a collision) hurt both parties, or games like democratic voting, in which one group of players can combine to benefit themselves at the expense of other players, he was less successful. He came up with a solution of a sort, but not a very useful one, since a single game might have anything from zero to an infinite number of solutions, and a single solution might incorporate up to an infinite number of outcomes. Later game theorists have carried the analysis a little further, but it is still unclear exactly what it means to solve such games and difficult or impossible to use the theory to provide unambiguous predictions of the outcome of most real-world strategic situations.
Economics, in particular price theory, deals with this problem through prudent cowardice. Wherever possible, problems are set up, the world is modeled, in ways that make strategic behavior unimportant. The model of perfect competition, for example, assumes an infinite number of buyers and sellers, producers and consumers. From the standpoint of any one of them, his actions have no significant effect on the others, so what they do is unaffected by what he does, so strategic problems vanish.
This approach does not work very well for the economic analysis of law; however tightly we may close our eyes to strategic behavior, we find ourselves stumbling over it every few steps. Consider our experience so far. In chapter 2, John was buying an apple that was worth a dollar to him from Mary, to whom it was worth fifty cents. What price must he pay for it? The answer was that it might sell at any price between fifty cents and a dollar, depending on how good a bargainer each was. A serious analysis of the bargaining—which, at that point, I deliberately omitted—would have led us to something very much like the game of Chicken, although with lower stakes. Mary insists she won't sell for less than ninety cents, John insists he won't pay more than sixty, and if neither gives in, the apple remains with Mary, and the potential gain from the trade disappears.
We encountered strategic behavior again in chapters 4 and 5, this time concealed under the name of transaction costs. When one farmer refuses to permit the railroad to throw sparks in the hope of selling his consent for a large fraction of what the railroad will save by not putting on a spark arrester, he is engaging in strategic behavior, generating what I called a holdout problem. So is the free rider who, under a different legal rule, prevents farmers from raising enough money to pay the railroad to put on the spark arrester. So is the railroad when it keeps throwing sparks and paying fines even though a spark arrester would be cheaper, in order to pressure the farmers to switch to clover.
One reason strategic behavior is so important in the economic analysis of law is that it deals with a lot of two-party interactions: litigation, bargaining over permission to breach a contract, and the like. When I want to buy corn I have my choice of thousands of sellers, but when I want to buy permission to be released from a contract the only possible seller is the person I signed the contract with. A second reason is that our underlying theory is largely built on the ideas of Coase, transaction costs are central to Coase's analysis, and transaction costs often involve strategic behavior.
Faced with this situation, there are two alternative approaches. One is to bite the bullet and introduce game theory wholesale into our work. That is an approach that some people doing economic analysis of law have taken. I am not one of them. In my experience, if a game is simple enough so that game theory provides a reasonably unambiguous answer, there are probably other ways of getting there.
In most real-world applications of game theory, the answer is ambiguous until you assume away large parts of the problem in the details of how you set it up. You can get mathematical rigor only at the cost of making real-world problems insoluble. I expect that will remain true until there are substantial breakthroughs in game theory. When I am picking problems to work on, ones that stumped John von Neumann go at the bottom of the stack.
The alternative approach, and the one I prefer, is to accept the fact that arguments involving strategic behavior are going to be well short of rigorous and try to do the best one can despite that. A first step in this approach is to think through the logic of games we are likely to encounter in order to learn as much as we can about possible outcomes and how they depend on the details of the game. Formal game theory is helpful in doing so, although I will not be employing much of it here.
In the next part of the chapter I work through the logic of two games: bilateral monopoly and prisoner's dilemma. Those two, along with closely related variants, describe a large part of the strategic behavior you will encounter, in this book and in life.
Mary has the world's only apple, worth fifty cents to her. John is the world's only customer for the apple, worth a dollar to him. Mary has a monopoly on selling apples, John has a monopoly (technically, a monopsony, a buying monopoly) on buying apples. Economists describe such a situation as bilateral monopoly. What happens?
Mary announces that her price is ninety cents, and if John will not pay it, she will eat the apple herself. If John believes her, he pays. Ninety cents for an apple he values at a dollar is not much of a deal—but better than no apple. If, however, John announces that his maximum price is sixty cents and Mary believes him, the same logic holds. Mary accepts his price, and he gets most of the benefit from the trade.
This is not a fixed-sum game. If John buys the apple from Mary, the sum of their gains is fifty cents, with the division determined by the price. If they fail to reach an agreement, the summed gain is zero. Each is using the threat of the zero outcome to try to force a fifty cent outcome as favorable to himself as possible. How successful each is depends in part on how convincingly he can commit himself, how well he can persuade the other that if he doesn't get his way the deal will fall through
Every parent is familiar with a different example of the same game. A small child wants to get her way and will throw a tantrum if she doesn't. The tantrum itself does her no good, since if she throws it you will refuse to do what she wants and send her to bed without dessert. But since the tantrum imposes substantial costs on you as well as on her, especially if it happens in the middle of your dinner party, it may be a sufficiently effective threat to get her at least part of what she wants.
Prospective parents resolve never to give in to such threats and think they will succeed. They are wrong. You may have thought out the logic of bilateral monopoly better than your child, but she has hundreds of millions of years of evolution on her side, during which offspring who succeeded in making parents do what they want, and thus getting a larger share of parental resources devoted to them, were more likely to survive to pass on their genes to the next generation of offspring. Her commitment strategy is hardwired into her; if you call her bluff, you will frequently find that it is not a bluff. If you win more than half the games and only rarely end up with a bargaining breakdown and a tantrum, consider yourself lucky.
Herman Kahn, a writer who specialized in thinking and writing about unfashionable topics such as thermonuclear war, came up with yet another variant of the game: the Doomsday Machine. The idea was for the United States to bury lots of very dirty thermonuclear weapons under the Rocky Mountains, enough so that if they went off, their fallout would kill everyone on earth. The bombs would be attached to a fancy Geiger counter rigged to set them off if it sensed the fallout from a Russian nuclear attack. Once the Russians know we have a Doomsday Machine we are safe from attack and can safely scrap the rest of our nuclear arsenal.
The idea provided the central plot device for the movie Doctor Strangelove. The Russians build a Doomsday Machine but imprudently postpone the announcement—they are waiting for the premier's birthday—until just after an American Air Force officer has launched a unilateral nuclear attack on his own initiative. The mad scientist villain was presumably intended as a parody of Kahn.
Kahn described a Doomsday Machine not because he thought we should build one but because he thought we already had. So had the Russians. Our nuclear arsenal and theirs were Doomsday Machines with human triggers. Once the Russians have attacked, retaliating does us no good—just as, once you have finally told your daughter that she is going to bed, throwing a tantrum does her no good. But our military, knowing that the enemy has just killed most of their friends and relations, will retaliate anyway, and the knowledge that they will retaliate is a good reason for the Russians not to attack, just as the knowledge that your daughter will throw a tantrum is a good reason to let her stay up until the party is over. Fortunately, the real-world Doomsday Machines worked, with the result that neither was ever used.
For a final example, consider someone who is big, strong, and likes to get his own way. He adopts a policy of beating up anyone who does things he doesn't like, such as paying attention to a girl he is dating or expressing insufficient deference to his views on baseball. He commits himself to that policy by persuading himself that only sissies let themselves get pushed around—and that not doing what he wants counts as pushing him around. Beating someone up is costly; he might get hurt and he might end up in jail. But as long as everyone knows he is committed to that strategy, other people don't cross him and he doesn't have to beat them up.
Think of the bully as a Doomsday Machine on an individual level. His strategy works as long as only one person is playing it. One day he sits down at a bar and starts discussing baseball with a stranger—also big, strong, and committed to the same strategy. The stranger fails to show adequate deference to his opinions. When it is over, one of the two is lying dead on the floor, and the other is standing there with a broken beer bottle in his hand and a dazed expression on his face, wondering what happens next. The Doomsday Machine just went off.
With only one bully the strategy is profitable: Other people do what you want and you never have to carry through on your commitment. With lots of bullies it is unprofitable: You frequently get into fights and soon end up either dead or in jail. As long as the number of bullies is low enough so that the gain of usually getting what you want is larger than the cost of occasionally having to pay for it, the strategy is profitable and the number of people adopting it increases. Equilibrium is reached when gain and loss just balance, making each of the alternative strategies, bully or pushover, equally attractive. The analysis becomes more complicated if we add additional strategies, but the logic of the situation remains the same.
This particular example of bilateral monopoly is relevant to one of the central disputes over criminal law in general and the death penalty in particular: Do penalties deter? One reason to think they might not is that the sort of crime I have just described, a barroom brawl ending in a killing—more generally, a crime of passion—seems to be an irrational act, one the perpetrator regrets as soon as it happens. How then can it be deterred by punishment?
The economist's answer is that the brawl was not chosen rationally but the strategy that led to it was. The higher the penalty for such acts, the less profitable the bully strategy. The result will be fewer bullies, fewer barroom brawls, and fewer "irrational" killings. How much deterrence that implies is an empirical question, but thinking through the logic of bilateral monopoly shows us why crimes of passion are not necessarily undeterrable.
Two men are arrested for a burglary. The District Attorney puts them in separate cells. He goes first to Joe. He tells him that if he confesses and Mike does not, the DA will drop the burglary charge and let Joe off with a slap on the wrist—three months for trespass. If Mike also confesses, the DA cannot drop the charge but will ask the judge for leniency; Mike and Joe will get two years each.
If Joe refuses to confess, the DA will not feel so friendly. If Mike confesses, Joe will be convicted, and the DA will ask for the maximum possible sentence. If neither confesses, the DA cannot convict them of the robbery, but he will press for a six-month sentence for trespass, resisting arrest, and vagrancy.
After explaining all of this to Joe, the DA goes to Mike's cell and gives the same speech, with names reversed. Table 8-1 shows the matrix of outcomes facing Joe and Mike.
Joe reasons as follows:
If Mike confesses and I don't, I get five years; if I confess too, I get two years. If Mike is going to confess, I had better confess too.
If neither of us confesses, I go to jail for six months. If Mike stays silent and I confess, I only get three months. So if Mike is going to stay silent, I am better off confessing. In fact, whatever Mike does I am better off confessing.
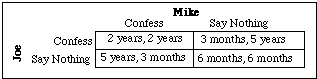
Table 8-1
Joe calls for the guard and asks to speak to the DA. It takes a while; Mike has made the same calculation, reached the same conclusion, and is in the middle of dictating his confession.
Both Joe and Mike have acted rationally, and both are, as a result, worse off. By confessing they each get two years; if they had kept their mouths shut, they each would have gotten six months. That seems an odd consequence for rational behavior.
The explanation is that Joe is choosing only his strategy, not Mike's. If Joe could choose between the lower right-hand cell of the matrix and the upper left-hand cell, he would choose the former; so would Mike. But those are not the choices they are offered. Mike is choosing a column, and the left-hand column dominates the right-hand column; it is better whichever row Joe chooses. Joe is choosing a row, and the top row dominates the bottom.
Mike and Joe expect to continue their criminal career and may find themselves in the same situation again. If Mike double-crosses Joe this time, Joe can pay him back next. Intuitively, it seems that prisoner's dilemma many times repeated, with the same players each time, should produce a more attractive outcome for the players than a single play.
Perhaps—but there is an elegant if counterintuitive argument against it. Suppose Joe and Mike both know that they are going to play the game exactly twenty times. Each therefore knows that on the twentieth play future retaliation will no longer be an option. So the final play is an ordinary game of prisoner's dilemma, with the ordinary result: Both prisoners confess. Since they are both going to confess on the twentieth round, neither has a threat available to punish betrayal on the nineteenth round, so that too is an ordinary game and leads to mutual confession. Since they are going to confess on the nineteenth .... . The whole string of games comes unraveled, and we are back with the old result. Joe and Mike confess every time.
Many people find that result deeply counter-intuitive, in part because they live in a world where people have rationally chosen to avoid that particular game whenever possible. People engaged in repeat relationships requiring trust take care not to determine the last play in advance, or find ways of committing themselves to retaliate, if necessary, even on the last play. Criminals go to considerable effort to raise the cost to their co-workers of squealing and lower the cost of going to jail for refusing to squeal. None of that refutes the logic of prisoner's dilemma; it simply means that real prisoners, and other people, are sometimes playing other games. When the net payoffs to squealing have the structure shown in table 8-1, the logic of the game is compelling. Prisoners confess.
For a real prisoner's dilemma involving a controversial feature of our legal system, consider plea bargaining:
The prosecutor calls up the defense lawyer and offers a deal. If the client will plead guilty to second-degree murder, the District Attorney will drop the charge of first-degree murder. The accused will lose his chance of acquittal, but he will also lose the risk of going to the chair.
Such bargains are widely criticized as a way of letting criminals off lightly. Their actual effect may well be the opposite—to make punishment more, not less, severe. How can this be? A rational criminal will only accept a plea bargain if doing so makes him better off, produces, on average, a less severe punishment than going to trial. Does it not follow that the existence of plea bargaining must make punishment less severe?
To see why that is not true, consider the situation of a hypothetical District Attorney and the defendants he prosecutes:
There are a hundred cases per year; the DA has a budget of a hundred thousand dollars. With only a thousand dollars to spend investigating and prosecuting each case, half the defendants will be acquitted. But if he can get ninety defendants to cop pleas, the DA can concentrate his resources on the ten who refuse, spend ten thousand dollars on each case, and get a conviction rate of 90 percent.
A defendant faces a 90 percent chance of conviction if he goes to trial and makes his decision accordingly. He will reject any proposed deal that is worse for him than a 90 percent chance of conviction but may well accept one that is less attractive than a 50 percent chance of conviction, leaving him worse off than he would be in a world without plea bargaining. All defendants would be better off if none of them accepted the DA's offer, but each is better off accepting. They are caught in a many-player version of the prisoner's dilemma, alias the public good problem.
Prisoner's dilemma provides a simple demonstration of a problem that runs through the economic analysis of law: Individual rationality does not always lead to group rationality. Consider air pollution, not by a few factories but by lots of automobiles. We would all be better off if each of us installed a catalytic converter. But if I install a converter in my car, I pay all of the cost and receive only a small fraction of the benefit, so it is not worth doing. In much the same fashion everybody may be better off if nobody steals, since we are all potential victims, but my decision to steal from you has very little effect on the probability that someone else will steal from me, so it may be in my interest to do it.
Constructing efficient legal rules is largely an attempt to get out of prisoner's dilemmas: criminal penalties to change the incentives of potential thieves, pollution laws to change the incentives of potential polluters. We may not be able to succeed completely, but we can at least try, whenever possible, to choose rules under which individual rationality leads to group rationality instead of rules that produce the opposite result.
I started this chapter with a very simple example of strategic behavior: two motorists approaching the same intersection at right angles. As it happens, there is a legal rule to solve that problem, one that originated to solve the analogous problem of two ships on converging courses. The rule is "Starboard right of way." The ship, or the car, on the right has the right of way, meaning that the other is legally obliged to slow down and let him go through the intersection first.
So far our discussion of games has yielded only two clear conclusions. One involves a version of bilateral monopoly in which each player precommits to his demands, pairs of players are selected at random, and the outcome depends on what strategies that particular pair has precommitted to. That is the game of bullies and barroom brawls, the game sociobiologists have christened "hawk/dove." Our conclusion was that increasing the cost of bargaining breakdown, making a fight between two bullies or two hawks more costly, decreases the fraction of players who commit to the bully strategy. That is why we expect punishment for crimes of passion to deter. Our other clear conclusion was that rational players of a game with the payoff structure of prisoner's dilemma will betray each other.
Even these results become less clear when we try to apply them to real-world situations. Real-world games do not come with payoff matrices printed on the box. Prisoner's dilemma leads to mutual betrayal, but that is a reason for people to modify the game, using commitment, reputation, altruism, and a variety of other devices to make it in each party's interest to cooperate instead of betraying. So applying the theoretical analysis to the real world is still a hard problem.
We can draw some other and less rigorous conclusions from our discussion, however. It seems clear that in bilateral monopoly commitment is an important tactic, so we can expect players to look for ways of committing themselves to stick to their demands. A small child says, "I won't pay more than sixty cents for your apple, cross my heart and hope to die." The CEO of a firm engaged in takeover negotiations gives a speech arguing that if he offers more than ten dollars a share for the target, he will be overpaying, and his stockholders should fire him.
Individuals spend real resources on bargaining: time, lawyers' fees, costs of commitment, and risk of bargaining breakdown. The amount they will be willing to spend should depend on the amount at stake—the same problem we encountered in our earlier discussion of rent seeking. So legal rules that lead to bilateral monopoly games with high stakes should be avoided where possible.
Consider, for a simple example, the question of what legal rules should apply to a breach of contract. Suppose I have agreed to sell you ten thousand customized cams, with delivery on March 30, for a price of a hundred thousand dollars. Late in February my factory burns down. I can still, by extraordinary efforts and expensive subcontracting, fulfill the contract, but the cost of doing so has risen from ninety thousand dollars to a million dollars.
One possible legal rule is specific performance: I signed the contract, I must deliver the cams. Doing so is inefficient; the cams are worth only $110,000 to you. The obvious solution is for us to bargain; I pay you to permit me to cancel the contract.
Agreement provides you a net gain so long as I pay you more than the $10,000 you expected to make by buying the cams. It provides me a net gain so long as I pay you less than the $900,000 I will lose if I have to sell you the cams. That leaves us with a very large bargaining range to fight over, which is likely to lead to large bargaining costs, including some risk of a very expensive breakdown: We cannot agree on a price, you make me deliver the cams, and between us we are $890,000 poorer than if you had let me out of the contract. That suggests one reason why courts are reluctant to enforce specific performance of contracts, usually preferring to permit breach and award damages, calculated by the court or agreed on in advance by the parties.
For another example, suppose a court finds that my polluting oil refinery is imposing costs on my downwind neighbor. One possibility is to permit the neighbor to enjoin me, to forbid me from operating the refinery unless I can do it without releasing noxious vapors. An alternative is to refuse an injunction but permit the neighbor to sue for damages.
If the damage to the neighbor from my pollution is comparable to the cost to me of preventing it, the court is likely to grant an injunction, leaving me with the alternative of buying permission to pollute from my neighbor or ending my pollution. If the cost of stopping pollution is much greater than the damage the pollution does, the court may refuse to grant an injunction, leaving my neighbor free to sue for damages.
If the court granted an injunction in such a situation, the result would be a bilateral monopoly bargaining game with a very large bargaining range. I would be willing, if necessary, to pay anything up to the (very large) cost to me of controlling my pollution; you would be willing to accept, if necessary, anything more than the (small) damage the pollution does to you. Where between those points we ended up would depend on how well each of us bargained, and each of us would have an incentive to spend substantial resources trying to push the final agreement toward his preferred end of the range.
Readers interested in a somewhat more extensive treatment of game theory will find it in chapter 11 of my Price Theory and Hidden Order. Readers interested in a much more extensive treatment will find it in Game Theory and the Law by Douglas G. Baird, Robert H. Gertner and Randal C. Picker, Cambridge, Mass: Harvard University Press 1994.