So far as I know, the only criticism of the Lott
and Mustard study to have appeared in a scholarly journal so far is
the article by Dan Black and Daniel Nagin in the January 1998
Journal of Legal Studies, although I am told that a second
article, by Ludwig, is forthcoming in the International Review of
Law and Economics. Since online criticisms of the study have
largely been based on versions of this article, I thought it would be
worth trying to summarize and discuss its contents in a form
accessible to non-statistician non-economist readers. Hence this
piece. My summaries of the Black and Nagin arguments are colored, to
distinguish them from my comments on them. I have EMailed a draft of
this page to both Black and Nagin, with a query as to whether I have
misrepresented their arguments, and the suggestion that they web
their article, but have not yet received any response.
Before explaining the article, it is worth sketching some very basic facts about statistics:
A multiple regression starts with a model, a guess at the relationship between a set of independent variables and a dependant variable. It then attempts to estimate how each independent variable affects the dependent variable, all other independent variables held constant.
The result is normally reported as two numbers. One is an estimate of the size of the effect, the regression coefficient--for a given increase in the independent variable, how much does the dependent variable change. The other is an estimate of how sure we are that the effect exists--how likely it is that our estimate of the regression coefficient would be as large as it is by pure chance. The latter is described as the significance of the result--in a typical regression result, it is measured by something called a t-statistic.
To understand the difference between the size of a result and its significance, consider a very simple experiment--flipping a coin to find out if it really comes up heads exactly half the time. Suppose you flip it ten thousand times, and it comes up heads 5100 times. The size of the effect is very small--the coin apparently comes up heads 51% of the time But with that many flips the chance that a fair coin would produce a result that far off of 50% is low, so the result is significant. The effect is small, but we can be pretty sure it is there.
Next suppose we had flipped the coin only ten times, and it came up heads six of them. The size of the effect is much bigger--it is coming up heads 60% of the time. But with only ten flips, a fair coin is quite likely to come up with six heads, so our confidence that the coin is biased is very low.
As this simple example suggests, an effect of a given size can generally be detected with greater confidence the larger the sample size--in this case, the number of coin flips. And the fact that an effect is statistically insignificant does not necessarily mean it is small--it may just mean that our data are not good enough to tell if it is large or nonexistent.
Many of Lott and Mustard's results, and Black and Nagin's, take the form of statements about coefficients and confidence. If Mustard and Lott are correct in their theoretical conjecture, coefficients relating confrontational crime rates (murder, rape, assault and robbery) to the existence of shall issue laws (laws requiring officials to issue permits for the concealed carry of handguns) should be negative--shall issues laws should, on average, reduce the rate of such crimes. Thus negative coefficients in the regressions are evidence in favor of their conjecture, positive against. But coefficients that are negative but insignificant are only weak evidence for their conjecture--the numbers are coming out in the right direction, but the effect might be due to chance.
Criticism 1: In the regression whose results are shown in Table 3 of the L&M article, one of the independent variables is the rate of arrests. This creates a problem, as Lott and Mustard point out, because for some counties for some years for some classes of offense, there are no offenses and no arrests, giving an arrest rate of 0/0. Such cases are omitted in the regression. This could conceivably bias the results, since it is omitting a non-random set of data--ones for counties with very low crime rates.
In order to eliminate this problem, Black and Nagin rerun the regressions, eliminating all counties with fewer than 100,000 people in them--and thus most of the counties for which this problem arises. Their results are generally similar to the results reported in Table 3. All of the predicted signs (for the effect of shall issue laws on Homicide, Rape, Assaults, and Robberies) are still negative, and the size of the effect is about the same--a little more for some crimes, a little less for others. The statistical significance of the results falls--as one would expect, since the change substantially reduces the amount of data being used. In the case of homicide, the number of observations falls from 26,458 to 6,009. This overstates the loss of information, however, since the regression is weighted by population; about 69% of the population of the full sample is included in the sample limited to counties of 100,000 or more.
Conclusion (mine): No evidence for any problem.
Criticism 2: The regression reported in Table 3 assumed that the size of the effect of shall issue laws was the same in all states. If the regression is done without this assumption, the state specific impacts vary from state to state by more than one would expect from random chance. In other words, the data give evidence that the size of the effect varied from state to state.
The results are shown in Table 1 of the Black and Nagin paper. Of the significant coefficients, 3 are positive (the opposite of what the Lott and Mustard argument predicts) and 12 are negative (consistent with their prediction).
Conclusion (mine): If Lott and Mustard's claim was that the effects were the same in all states, this would be evidence against it--but that is not their claim. In fact, they offer reasons why we would expect it to differ, not only state to state but county to county, and make some effort to look at such effects in other regressions that they report. Table 3 shows one relatively simple way of doing the regression--and like most specifications, it ignores some complications that might have been included in a more elaborate treatment. The results reported by Black and Nagin, however, support the conclusion Lott and Mustard are arguing for--that shall issue laws tend to reduce confrontational crime.
It is worth noting that the most striking evidence against the L&M thesis that appears on table 1 of the B&N paper--West Virginia, where the coefficient for homicides is large, positive, and statistically significant--has only one county with a population of more than 100,000, and that county has only 11% of the state's population. So what Black and Nagin give as the result for all the counties in the state is actually the result for a single county. A single random event--say the election of an incompetent county sheriff in the same year the shall issue law passed--could produce such a result--which is, of course, the reason for trying to set up regressions in ways that average effects across many counties.
Criticism 3: Black and Nagin point out that since effects vary by state, the overall result might be driven by some one state where something important other than shall issue laws was happening. They point to the Marial boat lift of 1980, when Castro exported a lot of people from his jails to Florida, and some new gun laws passed several years after the shall issue laws, and argue for eliminating Florida from the sample, reducing the number of states with shall issue laws from ten to nine. After eliminating Florida, limiting the sample to counties of more than 100,000, and rerunning the regression, three of the four coefficients are still negative (and the positive one is very small), but only one is statistically significant.
Comment (mine): The critical question here is whether there is a particularly good reason for eliminating Florida. If not, it looks as though what Black and Nagin have done is to try the regression with one state after another eliminated until they found a version that didn't work very well, and reported that--which is not very good evidence that the effect is not there.
Lott, in his reply, provides a graph of the Florida murder rate from which it appears that the effect of the boat lift had ended by about 1983. Prior to that, the murder rate is falling; from 1983 until 1987, when the shall issue law passed, the rate is constant to slightly rising. After the law was passed, the murder rate falls steadily and rapidly through 1991. 1992 is the year when Florida's waiting period and background check requirement went into effect. Furthermore, as Lott points out, 17 other states also had waiting periods by 1992, so why exclude Forida in particular? One of the other regressions in the Lott & Mustard article, not mentioned by Black and Nagin, included variables measuring the existence of such laws--and found that including them slightly strengthened the results.
It is also worth noting that the decision to set the population cutoff at 100,000 is to some degree arbitrary; a lower number could have eliminated many of the observations for which the arrest ratio was unavailable, with a smaller reduction in sample size. Alternatively, the regression could be run with all counties but without using arrest rates as an independent variable--one of the approaches that Lott and Mustard used.
Conclusion (mine): What Black and Nagin have shown so far is only that they were able to find some population cutoff which, combined with the elimination of a state of their choice, converts the results of one of Lott and Mustard's regressions from four coefficients out of four (for the four categories of confrontational crime) negative (the predicted sign), three of them significant, to three out of four negative, one significant.
Lott offers some further bits of evidence on this in his reply, on pages 234-235. In particular, he points out that the results get better if you look at the aggregate figure for all four crime categories, thus increasing the amount of data--a result that was reported in the Lott and Mustard table 3, but not in Black and Nagin's redo of the table 3 regression in table 1 of their paper.
Criticism 4: The regression shown in Table 3 of the Lott and Mustard paper assumed that a shall issue law had a once and for all effect--the dummy variable was one if such a law existed, zero otherwise. This ignores the (very likely) possibility that the effect would vary over time, presumably increasing as more and more people got handgun permits.
Black and Nagin accordingly reran the regression, using separate dummies for the effect five years before the law, four years before ... through five years after. Their dependent variable this time is not crime rate but change of crime rate. If Lott and Mustard are correct, and shall issue laws tend to reduce crime, we would expect that the coefficients would be smaller after the law than before. Black and Nagin found no such effect.
Comment (mine): Lott and Mustard in their original paper included the effect of changes over time--not in the regression reported on Table 3 but elsewhere in the article. They did so in two ways, one analogous to the approach used by Black and Nagin but different in detail (including the full sample of counties and a somewhat different set of control variables), and the other by looking at two states for which there were data on number of permits issued per year. It is a bit odd for Black and Nagin to provide their own analysis of the effect of changes over time without any discussion of the analysis of the same problem in the paper they are critiquing--especially since the paper found very different results than they did. I have no opinion on which version is more nearly correct.
Criticism 5: Having concluded that the regression shown in Lott and Mustard's table 3 does not adequately account for time trends, Black and Nagin reran the regression including both a linear and a quadratic time dependence. In other words, their equation for predicting the crime rate in each state includes a term of the form AiT+BiT2, where T is time and Ai and Bi are different for each state. With this included, they find no evidence for the Lott and Mustard thesis.
Comment (mine): Consider a state that started out with rising crime rates. If Lott and Mustard are correct, we would expect crime rates to rise until a shall issue law is passed, then to rise more slowly, or fall, with the effect increasing over time as more permits were issued and more criminals adjusted to the new facts. But a term of the form AiT+BiT2 can replicate that pattern, state by state. Thus Black and Nagin's result shows, not that the effect of the law is insignificant, but that the deviation of the law's effect from a quadratic curve over time is insignificant--with the parameters of the curve chosen to best fit that state's time pattern of crime rates.
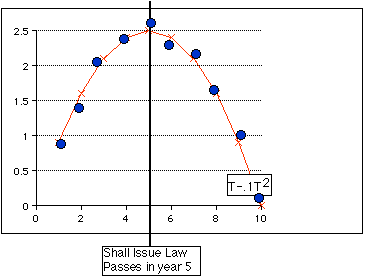
To illustrate the point, consider the figure; the
blue points show imaginary data for the crime rate in a state that
passed a shall issue law in year 5. The pattern clearly supports the
Lott and Mustard thesis--the crime rate is rising before the law and
starts falling immediately after. But that pattern can easily be fit
using a quadratic--as shown by the orange line, graphing the equation
T-.1T2, where T is the year. All that is left for the
regression to pick up as the effect of the law is the residual--the
difference between the blue dots and the orange curve, which shows no
particular pattern.

Conclusion (mine): This final point is utterly unconvincing--as some statistician is supposed to have said, "give me ten variables and I can fit the skyline of New York." The Lott and Mustard thesis implies a state specific time pattern in crime rates (because different states did or did not pass shall issue laws, or passed them at different dates). All Black and Nagin have shown here is that they can fit that state specific pattern with a state specific quadratic in time, well enough so that the residuals from the fit no longer have a pattern.
Overall conclusion (mine): I do not understand the different time trend analyses well enough to offer any judgement on whether Black and Nagin's initial method of doing it is better or worse than Lott and Mustard's similar but not identical way. Aside from that issue, the Black and Nagin critique is unconvincing. What they have shown is that:
1: The simplifying assumptions used in one of the regressions reported in the Lott and Mustard paper (Table 3) are not true--something that should be obvious to anyone who has read Lott and Mustard's original article, which included a variety of other regressions designed to deal with the complications assumed away in that one.
2: For one of the regressions reported by Lott and Mustard, there is a way of tinkering with the data set (eliminate all counties under 100,000 and the state of Florida), which substantially weakens the evidence for their thesis.
3. There is a way of analyzing the effect over time that does not support the Lott and Mustard thesis--but no discussion at all of the several ways in which Lott and Mustard analyzed the effect that did.
4. If you add a quadratic state dependent time variable the effect disappears--which we would expect to happen even if the Lott and Mustard thesis were true, for reasons I discuss above.
Back to my page
of links relevant to the
controversy
Back to my Home Page