Chapter 21

The Economics of Heating

At the beginning of this book, I defined economics as that way of understanding human behavior based on the assumption of rationality--that individuals have objectives and tend to choose the correct way to achieve them--and gave several simple examples. It may have occurred to you that if that is all economics is, economics is really nothing more than a straightforward application of common sense. It may have occurred to you since to wonder why it is necessary to load common sense with so heavy a burden of technical analysis: marginal cost curves, externalities, firm and industry equilibrium, and the like.

Using common sense to deduce the implications of rational behavior is not as simple as it might seem. So far, our techniques have been applied mostly to "textbook problems": hypothetical shipping industries, trade between Mr. A and Ms. B, and the like. In this chapter, I will apply some of those same tools to a set of real-world problems with which you are familiar--home heating. In the first part of the chapter, I demonstrate that two commonly observed features of heating behavior--decisions by homeowners concerning how warm to keep their homes--that seem inconsistent with common sense are actually implied, in a fairly simple way, by economic analysis. In the second part of the chapter, I will derive the profit-maximizing rule by which the owner of an apartment building should decide how warm to keep the apartments.

The purpose of this chapter is not so much to teach you how to heat your house, or even how to make money heating apartments, as it is to demonstrate that with the economics you now know, it is possible to derive surprising, interesting, and useful results about the real world.

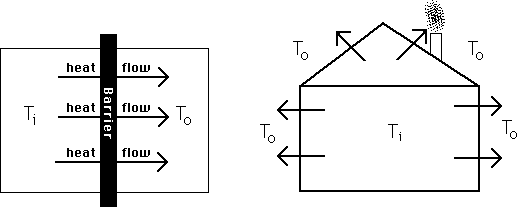
Before analyzing the economics of home heating, it is necessary first to say a little about the physics. Heat tends to flow from hot objects to cold ones. If the inside of your house is at 70° and the outside temperature is 0°, heat flows from the inside through the walls to the outside. In order to maintain the house at 70°, the heating system must put heat into the house as fast as it flows out--just as, in order to maintain the water level in a leaky tub, you must pour water in the top as fast as it comes out the bottom. The cost of maintaining a house at some particular interior temperature, given the external temperature, is simply the price of heat times the rate at which the house loses heat under those conditions.

There are three processes by which heat is transmitted from the inside to the outside of a house--or, more generally, from any object to any colder object. They are called conduction, convection, and radiation. The first, conduction is, for our purposes, both the most important and the easiest to analyze; so in this chapter I shall ignore the other two and discuss home heating as if conduction were the only way in which heat could be lost. Those students who are familiar with the physics of heat transmission may find it interesting to see to what degree the results can be generalized to include one or both of the others.

The physics of conduction is very simple. The rate at which heat flows through an insulating barrier--a wall, for example--is proportional to the temperature difference between the two sides of the barrier (T_i - T_o in Figure 21-1a). The formula is:

H = Heat Flow = C x (T_i - T_o). (Equation 1)

C depends in part on how good an insulator the barrier is. If the wall is well insulated, then C is small; only a little heat flows through it, even with a substantial temperature difference. If the wall is poorly insulated, C is large. C also depends on the dimensions of the barrier--the more area there is for heat to flow through, the greater the heat flow. Thus for the house shown in Figure 21-1b, C depends both on how well it is insulated and on its size and shape.

The cost of heating a house is the price of heat times the rate at which heat must be put into the house to make up for the heat flowing out through the walls. Hence:

TC_h = P_h x H = P_h x C x (T_i - T_o) (Equation 2)

where P_h is the price of heat and TC_h is the total cost of heating. TC_h is a rate, measured in dollars per day, just as H is a rate of heat flow, measured in BTUs per day. The price of heat depends on the cost of fuel oil, coal, electricity, or whatever input is used to heat the house and on the efficiency of the furnace, fireplace, or whatever is used to transform that input into heat.

---

Heat flow. Heat flows from a warmer object at a temperature of T_i to a cooler object at a temperature of T_o through an insulating barrier. The rate of flow is proportional to T_i - T_o; the proportionality constant depends on the barrier.

Figure 21-2 shows the implications of Equation 2 for several different houses. The total cost of heating each house is shown as a function of the internal temperature--the thermostat setting. TC₁, TC₂, and TC₃ correspond to identical houses with different external temperatures--0° for TC₁, 30° for TC₂, 60° for TC₃. TC₄ shows total cost for a better insulated house and TC₅ for a worse insulated house, both with an external temperature of 0° Since this chapter is concerned only with heating and not with air conditioning, the figure does not show any cost for internal temperatures lower than the external temperature.

As you can see by looking at Equation 2, the slope of the total cost curve is simply C x P_h; every time T_i goes up 1°, TC_h goes up by C x P_h. TC₁, TC₂, and TC₃ represent identical houses; the values of C and P_h are the same, so all three lines have the same slope. TC₄ is the total cost of heating a better insulated house, so its slope is less--the better insulated the house, the less additional heat required for each additional degree of internal temperature. TC₅ is the total cost of heating a worse insulated house, so its slope is steeper than the slopes of TC₁, TC₂, and TC₃.

The difference among TC₁, TC₂, and TC₃ is not the house but its environment. TC₁, TC₂, and TC₃ correspond to three different external temperatures--three different climates, or the same climate at three different times of the year. Looking at Equation 2, you can see that when T_i = T_o, TC_h is zero; it requires no heating to keep the temperature inside the house equal to the temperature outside. So TC₁, which shows total heating cost for a house with an external temperature of 0°, is zero for an internal temperature of 0°. TC₄ and TC₅ represent houses with the same external temperature as TC₁ so they are zero at the same internal temperature; all three lines intersect the horizontal axis at T_i = 0°. Similarly, TC₂ is zero at T_i = 30° and TC₃ at T_i = 60°.

---

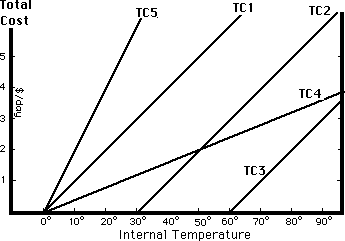
Total cost of heating various houses as a function of their internal temperature. 1, 2, and 3 are identical houses with different outside temperatures; 4 is a better insulated house and 5 a worse insulated one, each with the same outside temperature as House 1 (0°).

We are now finished with the physics of heating. We have learned two essential facts. The first is that maintaining a house at a constant temperature requires that heat be put in as fast as it flows out. The second is that the rate at which heat flows out is proportional to the temperature difference between inside and outside, with the constant of proportionality (C) depending on characteristics of the house such as size and insulation. The implications of those facts are shown in Equations 1 and 2 and Figure 21-2. With that, plus some economics, we are equipped to understand why people heat their houses as they do.

A native of Chicago who spends a winter in Los Angeles or Canberra is likely to find the houses uncomfortably cold and to express surprise that the natives are too stingy to heat their houses properly even though it would cost very little to do so. An Angelino wintering in Chicago or the Northeast is likely to have the opposite reaction; why, he wonders, do the inhabitants of such ferocious climates spend a fortune on overheating?

The pattern suggested by such casual observation--an inverse relation between external and internal temperature--seems inconsistent with both common sense and economic rationality. Home heating is more expensive in Chicago than in Los Angeles, so we would expect people to buy less of it, not more. If the opposite is observed, if houses are kept warmer in Chicago than in Los Angeles, that would seem to be evidence of irrational behavior.

Appearances are deceiving. Not only is the observed pattern consistent with rationality, it is implied by it. The "common sense" intuition in the opposite direction depends on a common economic error: confusion among different sorts of costs. Total heating cost, for any internal temperature, is higher in Chicago than in Los Angeles, but marginal heating cost is lower.

To see why this is true, we start by considering two identical houses in December. One is in Los Angeles, where the temperature outside is 60°; the other is in Chicago, where it is 0°. The houses are occupied by identical people, with identical tastes for internal temperature. Those tastes can be described by a marginal value curve, showing the value to the occupant of each additional degree of internal temperature. If, for instance, the occupant would be willing to give a maximum of $.15/day in order to have his house at 61° instead of 60°, then his marginal value for internal temperature is $.15/degree-day between 60° and 61°. If he would be willing to give only $.05/day to have the house at 71° instead of 70°, then at that part of the curve his marginal value for internal temperature is only $.05/degree-day.

Figures 21-3a and 21-3b show marginal value curve for two identical individuals, one in Los Angeles and one in Chicago. Since they are identical, their marginal value curves are the same; in each case the occupants favorite temperate--the temperature he would choose if the cost of temperature were zero--is 75.5°, where the MV curve intersects the horizontal axis. At temperatures below that, the occupant is willing to pay for more heat; at temperatures above, for less.

---

The marginal cost and marginal value of internal temperature for identical houses in Los Angeles (Figure 31-3a) and Chicago (Figure 21-3b). In each case, the occupant sets the thermostat to T*, where marginal cost equals marginal value. For internal temperatures above the external temperature, marginal cost is the same for both houses, so T* is the same in both cities.

Figures 21-3a and 21-3b also show the marginal cost curves faced by occupants in Los Angeles and Chicago. They are not identical. In Los Angeles the outside temperature is 60°; in Chicago it is 0°. Marginal cost, as you will remember from earlier chapters, is simply the slope of total cost. The total cost curves for the two houses are shown on Figure 21-2; TC₁ is the cost of heating the house in Chicago (outside temperature of 0°) and TC₃ the cost of heating an identical house in Los Angeles. As I pointed out earlier, TC₁ and TC₃, although they are different lines, have the same slope. The total cost of heating a house to, say, 70 ° is much higher when the external temperature is 0° than when it is 60° ; but marginal cost, the cost of keeping the house at 70° instead of 69° , or 71° instead of 70° , is not.

How can the marginal costs be the same when the total costs are not? The marginal costs are identical only for the upper part of their range. The inhabitant of Chicago and the inhabitant of Los Angeles pay the same amount for the additional cost of having a house at 69° instead of 68°, but the inhabitant of Los Angeles need pay nothing to have his house at 60°, while the inhabitant of Chicago pays for every degree above 0°

Faced with the situation shown in Figure 21-3, how does a rational occupant behave? He heats his house to that temperature for which MC = MV (T* on Figure 21-3a). If the house were colder than that, each additional degree by which he increased the thermostat setting would be worth more to him than it cost: MV > MC. If the house were hotter than that, each reduction of 1° would save him more on his heating bill than the value of the temperature he was giving up. We have seen this argument before. The individual's demand curve for internal temperature is the same as his marginal value curve for internal temperature, for exactly the same reason that the demand curve was the same as the marginal value curve in Chapter 4.

If you compare Figures 21-3a and 21-3b, you see that for temperatures above 60°, the MC curves are the same. Thus, as you can see from the figures, the optimal temperatures (T*) chosen by the occupants of the two houses are also the same. As long as we are considering internal temperatures which are higher than the external temperature in both cities--as long, in other words, as both occupants heat their houses--identical houses with identical occupants buying fuel at the same price will be heated to the same temperature in both Los Angeles and Chicago. The total cost of heating is much higher in Chicago, but the marginal cost is not--and it is the equality between marginal cost and marginal value that determines the optimal temperature.

So far, we have been considering identical houses in Los Angeles and Chicago. But houses in those two cities are not identical--not, at least, if their builders are rational. We have been analyzing the decision of where to set the thermostat; the next step is to analyze the decision of how to build the house.

One of the decisions made in designing a house is how much insulation to put in it. Insulation costs money. A rational builder who expects to live in the house himself will insulate it up to the point where the additional cost of one more inch of insulation is just equal to the resulting benefit in reduced heating bills. So will a rational builder who intends to sell the house; the lower the future heating bills are expected to be, the higher the price a rational customer is willing to pay for the house. This is an example of a point first made in Chapter 7; it is in the interest of a producer to make any quality improvement in his product that costs him less than the improvement is worth to the customer who buys the product.

Looking at Equation 2, you can see that, for any particular interior and exterior temperature, the total cost of heating is proportional to C. If you add together a series of costs, each of which is proportional to C, the sum is also proportional to C. So, for any pattern of future internal and external temperatures, the present value of hte total of all future heating bills is proportional to C. If, to simplify the mathematics, we ignore discounting (i.e., assume the interest rate is zero), the total cost of all future heating is simply the average value of T_i - T_o times P_h times C times the total number of years for which the house will be heated.

The lower the external temperature, the higher the cost of heating; the higher the cost of heating, the greater the savings from insulation. So the lower T_o is, the greater the savings from reducing C by adding more insulation. Since the cost of insulation is presumably about the same in Los Angeles and Chicago, and outside temperatures are, on average, much lower in Chicago, the rational builder will use more insulation in Chicago than in Los Angeles. Figure 21-4 shows a graphic analysis of the situation. The curve MC (the marginal cost of insulation, not, as before, of temperature) is the same in both cities; MV, the savings in heating bills due to each additional inch of insulation, is higher in the colder city. Th* is the optimal thickness of insulation. This time, the results of economics and of common sense are the same; houses are built with more insulation in Chicago than in Los Angeles.

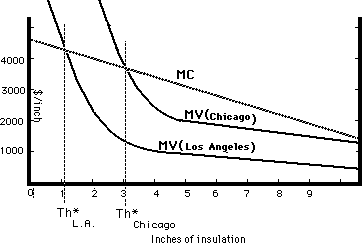
Marginal cost and marginal value of insulation in Chicago and Los Anbgeles. Marginal cost is the same in both cities; marginal value is higher in Chicago because the average temperature is lower there. Hence the optimal thickness of insulation, Th*, is greater in Chicago.

Figure 21-5 shows the final step of the argument. Since houses in Chicago are better insulated, the slope of the TC curve is lower; the curve representing the house in Chicago (on Figure 21-2) is TC₄ rather than TC₁. The marginal cost of heating does not depend on external temperature, but it does depend on how well insulated the house is; since houses in Chicago are better insulated than houses in Los Angeles, the marginal cost of internal temperature is less. It follows that the optimal internal temperature is higher. Looking at Figure 21-5, you can see that MC_Chicago intersects MV at a higher temperature than does MC_L.A.; T*_Chicago is greater than T*_L.A.. Houses in Chicago are warmer in winter than houses in Los Angeles.

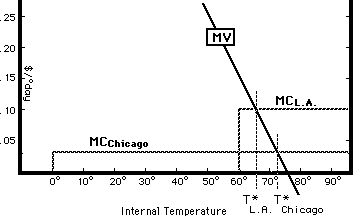
Marginal cost and marginal value of internal temperature for optimally insulated houses in Chicago and Los Angeles. The house in Chicago is better insulated, hence MC is lower and T* is higher than for the house in Los Angeles.

Exactly the same analysis explains a second paradox of rational heating. Just as it is more expensive to heat a house in Chicago than in Los Angeles, so it is more expensive to heat a house in Chicago in December than in September. The same intuition which suggests that houses in Chicago should be kept colder than houses in Los Angeles--because heating them "is more expensive"--also suggests that houses in Chicago should be kept colder in winter than in fall.

Here again, economics and "common sense" give different answers--not because economics is irrational but because "common sense" has not thought the question through carefully enough. Figures 21-3a and 21-3b were originally drawn to show two identical houses in different places at the same time, but they could just as easily show the same house in the same place at different times. The cost of keeping a particular house in Chicago at 70° instead of at 69°--the marginal cost of internal temperature--is the same whether the temperature outside is 60° or 0°. So the optimal internal temperature is also the same. The rational decision is to keep the thermostat at the same setting throughout the heating season--which is what, in my experience, most people do.

So far, I have discussed the problem on the assumption that people in Los Angeles and Chicago are identical. That corresponds to the way my observations were made; when I visit in Los Angeles, I visit the same sort of people, in terms of income and tastes, as I visit in Chicago. When I lived in Los Angeles, I was the same person as when I was living in Chicago.

It might be argued, however, that there is one large and relevant difference between people in Chicago and people in Los Angeles: their heating bills. Similar people with similar incomes will have different amounts left after paying for heating in the two cities. Does this not mean that people in Chicago are, in effect, poorer, hence value money more (higher marginal utility of income), hence have a lower MV curve--since the MV curve measures the value for temperature in terms of money?

Not necessarily. If similar people, with similar skills and tastes, were better off in Los Angeles than in Chicago, one would expect people living in Chicago to move west. As they did so, the decreasing population would drive down property values in Chicago while the increasing population drove up property values in Los Angeles, making Chicago a more attractive place to live in than before and Los Angeles less attractive. In equilibrium--equilibrium, this time, of population distribution--the two cities must on net be equally attractive. If they were not, it would be in the interest of some people to move--which would mean that we were not yet in equilibrium.

You should by now be getting a feel for the complication and fascination of this sort of analysis. Equilibrium sounds like a simple idea when we are merely crossing two lines on a graph. But individuals and markets in the real world are in equilibrium, or tending toward equilibrium, in many different dimensions; marginal cost and marginal value are being equated simultaneously on many different margins. In solving the problem of home heating, we have used three simultaneous equilibria, resulting from rational behavior with regard to three different choices: thermostat setting, insulation, and where to live.

There is one interesting case in which the argument from migratory equilibrium does not hold. Suppose fuel costs rise sharply and unexpectedly--as they did after the Arab oil boycott. The result is to increase the relative advantage of Los Angeles over Chicago; since fuel is more expensive, the difference in the total cost of heating in the two cities is higher than before. People begin moving west. Property values in Chicago (and Boston and Cleveland and . . .) go down. The newspapers start talking about a land boom in the Sunbelt.

But most of the property, or at least most of the residential real estate, in Chicago belongs to people who live in Chicago. Suppose I am such a person; I live in Chicago in a house I own. So far as my incentive to move is concerned, the fall in housing costs fulfills exactly the same function for me as for a tenant renting an apartment. If I move to Los Angeles, I must sell my present house at a low price and buy a house in Los Angeles at a high price--which is a reason for me not to move, just as having to give up a low-rent apartment in Chicago and move into a high-rent apartment in Los Angeles is a reason for a tenant not to move. But so far as my welfare is concerned, the effect is quite different. The low rent in Chicago, after fuel prices have just risen, compensates tenants for their increased heating costs. But the fall in the market value of my house is no compensation for higher heating bills if I own the house.

The fact that heating is expensive in Chicago does not make people in Chicago poor, but the fact that it has just become unexpectedly more expensive does. As people move out, the value of assets that cannot move--houses, in my example, but also firms with a local reputation, employees with experience working in a particular local job (firm-specific human capital), and the like--goes down. Most of those assets belong to people in Chicago, so people in Chicago are, on average, worse off than before. When people are poorer, they buy less of most things, including heat. The increased cost of heating drives down thermostats in both Los Angeles and Chicago, but in Chicago the substitution effect of a higher marginal cost of heating is reinforced by a substantial income effect. Houses in the Midwest and the Northeast were very cold in the winter of 1971-2.

You are a landlord; you own a building containing two apartments, both of which you rent out. How should you decide how warm to keep the apartments?

Before answering this question, we should first ask why (aside from legal requirements) you want to heat the building at all. The answer is that if you do not, no one will rent your apartments. This suggests a further question: exactly how is the amount you can get for your apartments affected by how warm you keep them?

Suppose that other landlords offer apartments just like yours, heated to a temperature of 68°, for $200/month. The rental market is competitive; if you too heat your apartment to 68°, you can get all the tenants you like at $200/month, and none at any higher rent.

Tenants value apartments for many different characteristics--including their temperature. Just as in Part 1 of this chapter, a tenant's taste for internal temperature may be represented by a marginal value curve. The total value to him of increasing the temperature from 68° to 73° is the sum of the marginal values for each little increase in temperature along that range--the area B under the MV curve between 68° and 73°, as shown on Figure 21-6. The analysis is just like the analysis that originally gave us consumer surplus. Since, at this point in the discussion, the landlord is paying for the heat, the difference in surplus to the tenant between a temperature of 68° and of 73° is the full area under the curve, not just the area between MV and P.

But if a change in temperature, as from 68° to 73°, changes the total value the tenant receives from the apartment, it also changes the maximum rent he is willing to pay. The area under a marginal value curve between one quantity and another shows the difference in what a consumer is willing to pay for the different quantities, as we saw first in the explanation of consumer surplus in Chapter 4 and later in the analysis of two-part pricing in Chapter 10. So, a tenant who was willing to pay $200/month for an apartment heated to 68° should be equally willing to pay $200 + B for the same apartment heated to 73° or $200 - A for the apartment heated to 63°.

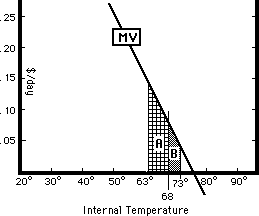
The effect on rent of changes in the internal temperature of an apartment. MV shows the marginal value of temperature to the tenant. A is the decrease in the maximum rent he will be willing to pay if temperature is at 63° instead of 68°; B is the increase if it is at 73° instead of 68°.

You, the landlord, now have a choice. You can offer better heated apartments than your competitors do and charge higher rents; you can offer cooler apartments and charge lower rents. The change in the rent you can collect (i.e., the highest rent at which you will be able to find tenants) will be equal to the change in consumer surplus on Figure 21-6. You maximize your profit by raising the temperature of the apartment as long as the resulting increase in surplus, and hence rent, at least balances the increased cost of heating. Here, just as in the Disneyland case discussed in Chapter 10, what starts as consumer surplus (on rides in Disneyland, on temperature in your apartment building) ends up as revenue to the producer (entry price in Disneyland, rent on the apartment).

Identical Tenants, Identical Apartments. Assume that all tenants are identical; each has the MV curve shown in Figure 21-6. Further assume that the marginal cost of internal temperature is P (= C x P_h in the first part of the chapter). I call it P because it is the price you pay for each degree of internal temperature that you buy for your tenants.

With these assumptions, the solution to the problem of heating a building with two identical apartments is simple. Since each 1° increase in temperature benefits each tenant by MV, the total benefit from each 1° increase--which you can collect in higher rents--is 2 x MV. Heat the building to the temperature T*, at which 2 x MV = P. The analysis should by now be familiar. At any lower temperature, 2 x MV > P, so an increase in temperature increases total surplus, and hence rent, by more than it increases heating cost. So if the temperature is less than T*, it is in your interest to increase it; you will be able to raise the rent by more than the increase in your heating bill and still find tenants. At any temperature above T*, 2 x MV < P, so a decrease in temperature decreases total surplus, and hence rent, by less than it decreases heating cost. If the temperature is higher than T*, it is in your interest to lower the temperature; the savings on your heating bill will more than compensate you for the reduction in the rent you can get for the apartments. If the temperature is lower than T*, it pays to raise it; if it is higher than T*, it pays to lower it. So the optimal temperature , from your standpoint, is T*.

Identical Apartments, Different Tenants. To make the problem more interesting, I now drop one of the simplifying assumptions--the assumption that both tenants have the same tastes for temperature (identical MV curves). The new situation is shown by Figure 21-7; MV₁ represents the tastes of Tenant 1 and MV₂ the tastes of Tenant 2. The marginal value of internal temperature to you is MV₁ + MV₂; that is the amount by which the value of the apartments to your tenants, and hence the rent you can charge without losing them, increases for each degree by which you increase the temperature of the building. To find the optimal (i.e. , profit-maximizing) temperature, you merely find the intersection of MV₁ + MV₂ with P, as shown (at T*) on Figure 21-7.

This is the correct answer if you assume that both apartments must be at the same temperature. Suppose, however, that you can separately control the temperatures of the two apartments. If the apartments are identical, as in the building shown in Figure 21-7, then the cost of heating each apartment is simply P/2 per degree. Heat can only be lost through the external walls; since each apartment has half the external walls of the whole building, the heat loss to the outside from holding Apartment 1 at a temperature T₁ is simply half what the heat loss would be from holding the whole building at that temperature.

I specified the heat loss to the outside. If T₁ is higher than T₂ (as shown in Figure 21-8), heat will also flow through the wall between the apartments; the rate at which you must put heat into Apartment 1 in order to maintain it at T₁ is then more than half what would be needed to hold the whole building at T₁. But that additional heat loss from Apartment 1 costs you nothing; every dollar spent to replace heat that flows through the interior wall is a dollar less spent heating Apartment 2. Hence the net cost to the landlord of each extra degree of interior temperature in Apartment 1 (or 2) is only the cost of the heat lost to the outside: P/2.

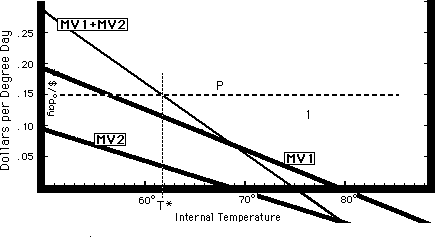
Finding the optimal internal temperature for a building with two tenants. The two apartments are identical; the tenants are not. The landlord maximizes his profit by heating the apartment to a temperature T* at which P, the cost of internal temperature, equals MV₁ + MV₂, the total marginal value of temperature to the tenants.

A building with two identical apartments. T₁ is the internal temperature of Apartment 1, T₂ is the internal temperature of Apartment 2, and T_o is the temperature outside the building. Heat flows from both apartments to the outside and from the warmer apartment (1) to the cooler (2).

The cost to the landlord of each degree of temperature in Apartment 1 is P/2; the benefit is MV₁, received by the tenant but transmitted, in the form of higher rent, to the landlord. Profit is maximized at a temperature T₁* where MV₁ = P/2. Similarly, for the second apartment, profit is maximized at T₂* with MV₂ = P/2. The solution is shown in Figure 21-9; profit is increased, relative to the result shown on Figure 21-7, by the colored areas.

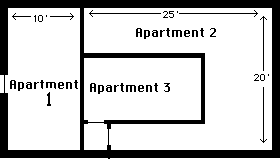
Different Apartments, Different Tenants. The problem has been solved in a particularly simple case: a building with two identical apartments. The solution can easily be generalized. For each apartment, calculate the marginal cost of internal temperature, ignoring any heat loss that goes to other apartments. If, for the single-story apartment building shown in Figure 21-10, we ignore heat losses through the roof and ceiling, teh cost for each apartment is proportional to its external wall area, as shown in Table 21-1. Note that apartment 3 has no exterior walls; hence the marginal cost of heating it is zero--any heat lost goes into one of the other apartments. It should be heated to the temperature at which marginal value of internal temperature is zero. Figure 21-11a shows how the building should be heated: P₁ is the price of each degree of internal temperature in Apartment 1, P₂ in Apartment 2, P₃ in Apartment 3; T₁ is the optimal temperature for Apartment 1, T₂ for Apartment 2, T₃ for Apartment 3. For more realistic three-dimensional cases, in which heat can be lost in any direction, the calculation of the marginal cost of heating each apartment is more complicated. But once the marginal cost has been calculated (by a physicist or a building engineer, not an economist) the profit-maximizing temperature is found in the same way.

We are not yet done. So far, I have assumed that you have perfect knowledge both about the rent tenants are willing to pay and about their taste for temperature, as shown by their MV curves. The first half of the assumption is realistic enough in a competitive market; you can determine the highest price anyone is willing to pay for an apartment by posting a high rent and gradually lowering it until you get a tenant. Determining your tenant's taste for heat is a more difficult problem. I will therefore drop the second half of the assumption. From here on, we will assume that whatever temperature you heat the apartment to, you will always collect the highest rent your tenant is willing to pay, but that you know nothing at all about his taste for temperature.

---

Even if you do not know the tenant's taste for temperature, he does. To use that knowledge, you install a thermostat in each apartment and let the tenant set it to whatever temperature he prefers. What happens?

Two Wrong Answers. One possibility is shown in Figure 21-11b. Here the tenant sets the interior temperature while the landlord continues to pay the heating bill. The tenant of Apartment 1 sets his thermostate to T_a, the point for which the marginal value of temperature to him reaches zero; since he is not paying for internal temperature, he consumes it as long as it has any value at all. This is inefficient (and unprofitable) compared to the optimal solution (T₁) shown in Figure 21-11a, since some of the temperature the tenant consumes is worth less to the tenant than it costs the landlord to produce. The loss of profit on Apartment 1, relative to the solution shown in Figure 21-11a, is shown as the colored area on Figure 21-11b. It is the difference between the value to the tenant of the additional temperature between T₁ and T_a (the gray shaded area) and its cost to the landlord, P₁ x (T_a - T₁ ).

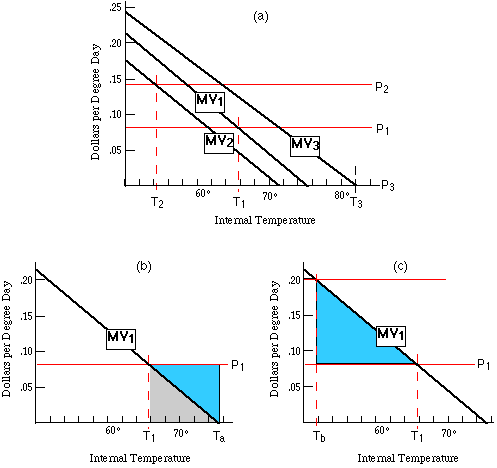
A second possibility is shown in Figure 21-11c. Here the tenant not only sets the thermostat, he also pays the bills. Each apartment is heated by its own electric heater, and the cost is part of the tenant's electric bill. The figure shows the result for Apartment 1.

This result is also inefficient --and unprofitable--compared to the solution shown in Figure 21-11a. In Figure 21-11b, the apartment is too hot, since the tenant sets the thermostat as if heat were free. In Figure 21-11c, it is too cold. The cost to the tenant of raising the temperature of his apartment is equal to the cost of the additional flow of heat necessary to maintain the higher temperature. When he turns up his thermostat, the result is to increase not only the heat loss to the outside but also the heat loss to the other apartments; since internal walls are usually less well insulated than external walls, the increased heat loss to the other apartments may be several times as great as the increased heat loss to the outside. In drawing Figure 21-11c, I have assumed that C_i, the constant describing heat conduction from the apartment to other apartments, is three times as great as C_o, the corresponding constant for heat loss to the outside world.

In order to simplify the next few paragraphs, I will define C_i C_i x (area of internal walls) and C_o C_o x (area of external walls). For Apartment 1, C_i = 1.5 x C_o. Obviously, C_i and C_o will vary from one apartment to another, but since we will for the most part be discussing only Apartment 1, this will not matter.

Remember that here, just as in the first part of this chapter, what determines the choice of temperature is not total cost but marginal cost. If the apartment is at 70deg., the adjacent apartments at 65 deg., and the outside world at 0deg., total heat loss to the outside will be much larger than total heat loss to the other apartments. But if the internal temperature is increased by 1deg., heat loss to the outside goes up by 1deg. x C_o, heat loss to the inside goes up by 1deg. x C_i; so the marginal heat loss to the other apartments is 1.5 times the marginal heat loss to the outside. The total cost of maintaining the apartment at 70deg. consists largely of the cost of replacing heat lost to the outside, but 60 percent of the marginal cost--the cost of heating to 71deg. instead of 70deg.--comes from the increase in the amount of heat lost to the other apartments.

This is true even if the other apartments are hotter, not colder, than the apartment we are considering. Heat flow is proportional to the temperature difference between the two sides of the wall, as shown in Equation 1. If Apartment 1 is at 70° and the adjacent apartments are at 75°, heat is flowing from them into Apartment 1. If the temperature of Apartment 1 goes up to 71°, the heat flowing into it decreases--by 1deg. x C_i. A decrease in the amount of heat you are getting--for free--from the neighboring apartments increases your heating bill, just as an increase in the heat you are losing to the neighboring apartments would. Whether the adjacent apartments are warmer than Apartment 1, cooler, or soem warmer and some cooler, each degree by which the tenant of Apartment 1 raises his thermostat costs him P_h x ( C_i + C_o ) in additional electricity. That is the price, to him, of temperature; he maximizes his consumer surplus by choosing the temperature, T_b, for which MV = P_h x ( C_i + C_o ).

With the values of C_i and C_o which I have assumed, the cost that tenant 1 pays to raise the temperature of his apartment is about two and one half times the cost to the landlord; out of each five BTU's he puts into raising the temperature of his apartment, three flow through the interior wall and end up lowering his neighbors' heating bills. That ultimately benefits the landlord; the lower the heating bills for his apartments, the more rent people will be willing to pay for them. From the standpoint of the tenant, the marginal cost of raising the temperature of Apartment 1 by 1deg. is P_h x ( C_i + C_o ); from the standpoing of the landlord, it is only P_h x C_o .

The Right Answer. How does the landlord produce the result shown on Figure 21-11a without knowing MV, the tenant's marginal value curve for temperature? By letting the tenant set the thermostat and then subsidizing his heating bill. Of every $5 wpent on heating Apartment 1, the landlord pays $3 and the tenant $2. From the standpoint of the tenant, the cost of interior temperature to the tenant is now P_h x ( C_i + C_o ) /2.5 = P_h x C_o =P₁. He maximizes his consumer surplus (from buying temperature) at T₁

At this point, you may be feeling somewhat confused about the contract between landlord and tenant. If the rent is a function of the tenant's surplus, which in turn depends on the temperature he sets his thermostat at, should he not take that as well as his heating bill into account in deciding what temperature to keep his apartment at? The answer is no. The tenant is frenting the apartment for a fixed rent, say $200/month. Given that he is doing so, he sets his thermostat at whatever temperature maximizes his surplus from buying temperature --T_a if the landlord pays the heating bill, T_b if the tenant pays it, T₁ if it is split in the way I have described.

What determines the rent? The amount that other, similar, potential tenants are willing to pay. What determines that? Among other things, the surplus they would receive, if they rented the apartment, from buying temperature on whatever terms the landlord is offering it at. So the rent includes the surplus a tenant can get. If one tenant chooses to buy less (or more) temperature than the "optimal" level under the arrangements of Figures 21-11a, 21-11b, or 21-11c, he finds that the apartment, which was just worth renting if he bought the optimal amount of temperature, is now no longer worth renting; either he readjusts his thermostat or he gives up the apartment to another tenant.

It is up to the landlord to determine on what terms he should sell temperature (and housing) so as to maximize his total profit--rent minus his expenditue on heating (and other operating expenses irrelevant to this discussion). What I have shown is that the rule which maximizes his profit is to sell temperature "at cost." The logic of the situation is the same as the logic of perfect discriminatory pricing (Chapter 10), discussed there in terms of cookies and Disneyland. What is special in this case is that the cost of internal temperature to the tenant, if he provides it himself, is greater than the cost tothe landord; so the landlord "sells temperature at cost" by subsidizing the tenant's heating bill.

So far, I have discussed the problem as an exercise in perfect discriminatory pricing. There is another and equally valid way of looking at the same problem and deriving the same result--in terms of externalities.

We start by ignoring the landlord and considering the situation of Figure 21-11c (tenant pays his own heating bill) from the standpoint of the tenant. He is deciding on the temperature of his apartment by rationally balancing cost and benefit; he increases the temperature up to the point where an additional degree is worth just what it costs him (T_b). Why is this unsatisfactory?

It is unsatisfactory because every time he raises his thermostat, he provides positive externalities to his neighbors--the warmer his apartment is, the more heat flows from it into theirs (or the less from theirs into it), hence the lower their heating bill. As I explained in Chapter 18, a good with positive externalities (a mowed lawn, a handsome skyscraper, basic research) is underproduced. The producer produces only up to the point where his marginal benefit is equal to the marginal cost of production, rather than up to the point where the total marginal benefit, including the external benefit received by other people, equals marginal cost. That is precisely the outcome shown on Figure 21-11a. Temperature of Apartment 1 is underproduced; T_b is less than T₁.

The "textbook solution" to the underproduction of goods with positive externalities is to subsidize them, paying the producer an amount equal to the external benefit. His gain from each unit produced is then equal to internal gain (his value for consuming it or the price for which he can sell it) plus external gain; so he produces up to the point where total marginal benefit, external plus internal, equals marginal cost. That is precisely the result shown in Figure 21-11b. The tenant of apartment 1 is receiving a subsidy of P_h x C_i for each degree of temperature he produces. P_h x C_i is just equal to the value of the increased heat flow to the other apartment resulting from a 1deg. increase in the temperature of Apartment 1.

We have gotten to the same place by two quite different routes. The first argument derived the optimal rule from the behavior of a landlord trying to maximize his profit; the second derived the same rule from the policy that leads to the efficient level of production of a good that generates positive externalities. Why are the results the same?

The answer has been given already, back in Chapter 15. Under conditions of perfect discriminatory pricing, all of the benefits from the good in question end up in the pocket of the seller. Hence the arrangements that maximize net benefit (are Marshall efficient) also maximize his profit, and vice versa.

There is one important difference between this chapter and the previous discussions of discriminatory pricing. In all the previous cases, the discriminatory pricing was done by a monopolist. In this case, the landlord is a monopolist only in the sense of having a monopoly over the heating of his own apartment building; otherwise the rental market is assumed to be perfectly competitive. The consumer surplus which the landlord "pockets" is the surplus due to the tenant renting that particular apartment rather than some other apartment. It is positive only if the landlord has some advantage over his competitors--perhaps because he has read this chapter and they have not.

The demonstration in this chapter that a landlord will find it in his interest to produce an efficient level of heat is really a special case of the demonstration, in Chapter 7, that landlords will find it in their interest to make all improvements, and only those improvements, which are worth at least as much to the tenant as they cost the landlord. Just as in that case, the landlord gets an above-market return from making such improvements only if, for some reason, his competitors do not make them. If everyone sees, and follows, the logic of this chapter, the competitive housing industry, like other competitive industries with open entry, finds that the maximum profit it can make is zero. The gains produced by the improvement are then divided between the owners of the inputs to the housing industry--urban land, for instance--and its consumers.

If my analysis is correct, a landlord who followed the policy I describe would increase his profit--the additional rent would more than repay the cost of the subsidy. If so, others would imitate him; the ultimate result would be a rental industry in which such subsidies were common practice, at least for those buildings where it was practical to separately control and separately bill the heating of different apartments. If, as I have argued, the result would be a Marshall improvement, where would the improved efficiency come from?

It would come in two ways. The first, and more obvious, is the efficiency gain shown in muy figures. Buildings in which the previous rule was to heat all apartments to the same temperature (Figure 21-7) would save by eliminating the overheating of apartments occupied by tenants with a low MV for temperature and the underheating of those occupied by tenants with a high MV for temperature. They would also gain by increasing the temperature of apartments that were inexpensive to heat, such as Apartment 3 on Figure 21-10, and lowering the temperature of apartments that were expensive to heat. Buildings in which the previous rule was "tenant controls, landlord pays" (Figure 21-11b) would eliminate the resultant overheating; those where the rule was "tenant controls and pays" (Figure 21-11c) would eliminate underheating. In each case, temperatures would rise if the value of additional temperature was more than its cost and fall if it was less; both changes represent net gains.

There would be another efficiency gain as well. Consider Apartment 3 in Figure 21-10. Since it is entirely interior to the building, it costs nothing to heat it; any heat that flows out of it flows into another apartment (I fudged the numbers a little by ingoring heat loss through the door). Under the system I have described, the landlord would pay the entire heating bill for Apartment 3.

Given that he did so, its relative attractiveness would be greater for a tenant who wanted an unusually warm apartment, so it would probably be rented by such a tenant. Apartment 2, on the other hand, which has an unusually large amount of external wall, would be expensive to heat and would receive a low subsidy; it would be relatively more attractive to tenants who intended to keep their apartment cool.

The overall result would be a more efficient allocation of tenants to apartments, with those tenants who liked warm apartments tending to end up in apartments that were inexpensive to heat--at higher rents, of course--and those who liked cool apartments ending up in those that were expensive to heat. This is a second, and less obvious, efficiency gain resulting from the arrangements I have described.

It may have occurred to you that in this second part of the chapter I am not describing but prescribing. So far as I know, heating subsidies are not normal practice in apartment buildings, not even in buildings where it is practical for each tenant to control, and pay for, his own heat. If so, that is evidence either that my analysis is wrong or that the market is, in this instance, failing to produce the efficient--and profit-maximizing--outcome.

I argued in Chapter 1 that economists assume rationality not because it is true but because it is useful; people are in part rational, and it is their rationality that provides the predictable element in their behavior. This implies that irrationality is not very useful, since it is unpredictable, but not that it does not exist. Perhaps the absence of heating subsidies is the result of irrationality on the part of either landlords or tenants.

It is a dangerous policy for an economist to explain divergences between his predictions and his observations of the real world as instances of irrationality. Such divergences may, after all, be evidence that the economic analysis is mistaken; if we automatically shrug them off as irrational, we are abandoning our best tool for spotting our own mistakes. It is a particularly dangerous policy given that economists, like other people, are reluctant to believe that they have made a mistake.

On the other hand, if all of us, economists and economic actors alike, assume that whatever is currently being done must be correct, then we will never discover better ways of running our businesses or our lives. This suggests that every economist should wear two hats. As an economist, he should assume that all observed behavior is rational and treat any divergence between what his analysis predicts and what he observes as evidence that the analysis is wrong. As a participant in the economy, an economic actor, he should assume that it is up to him to figure out what is rational in order to decide what to do. Economic theory, which consists largely of figuring out how a rational individual would act, is a useful tool in doing so. If, as in the second part of this chapter, his conclusion is that there is a better way of running a business than the way it is being run, he should regard that not as an anomaly but as a profit opportunity.

Economics Joke #4: A professor of economics and a graduate student were walking down the street. "Look," the student said, "there is a $10 bill on the sidewalk." "Nonsense," the professor replied. "If there had been a $10 bill on the sidewalk, someone would have picked it up." (This is an example of the application, and limitation, of the assumption of rationality)

The argument for this sort of "double vision" was brought home to me some years ago when I was a member of the board of directors of a company that ran health spas. It was common practice in the health spa industry (and nonprofit equivalents, such as YMCA's and country clubs) for firms to sell their services in the form of memberships--long-term, nonrefundable contracts. The Federal Trade Commission was trying to force the industry to offer the customers short-term contracts, which the customers could cancel if they found that they did not like the product.

In the course of their campaign, the FTC produced a piece of economic analysis which appeared to demonstrate that the introduction of cancelable contracts would lead to a net efficiency gain--a Marshall improvement. Although the article did not say so, its analysis also implied that a spa which offered such contracts--and charged the customers a higher price for the more desirable product--would increase its profits. The author missed that conclusion because he assumed that the new contract would be sold for the same price as the old, even though the option of withdrawing from the spa and getting a refund would make the new contract a more attractive product. He was guilty of what I described in Chapter 2 as naive price theory: assuming prices do not change when there is a good reason why they should.

I found myself in an odd position. As an economist, my assumption was that the firms in the industry knew how to maximize their profits and did so; the problem was to explain why the present policy of long-term, nonrefundable contracts was correct. As a member of the board of directors of one such firm, it was my business to help figure out how the firm could maximize its profits--which was hardly consistent with assuming it was already doing so.

My response, as an economist, was to write an article providing a plausible, although not necessarily correct, justification for the way the industry was selling its product. My response as a member of the board was to try to persuade management to experiment with refundable contracts. I failed; management, like its opponents in the FTC (and possibly for the same reasons) was persuaded that the present policy maximized its profits. A year or two later, the firm was partly taken over by a very successful group of health spa companies--one of whose innovations was offering short-term contracts.

1. Throughout the chapter, I have ignored air conditioning.

a. Redraw Figure 21-2 on the assumption that using air conditioning to take heat out of a house costs the same amount ber BTU as using a heating system to put heat into a house.

B. If we included the effect of air conditioning, would hte conclusion of Part 1 of the chapter--that houses in warmer climates are kept cooler in winter than houses in colder climates--be affected? Discuss.

2. In analyzing how you should heat your apartment building, I asumed that your competitors were charging $200/month for similar apartments and heating them to 68deg.. If I change one or both of those numbers, will the result be to change the rent you should charge, the temperature you should heat the apartments to, both, or neither? Explain.

3. Assume that all tenants have the marginal value curve for temperature shown by Figure 21-6. Your apartment building has two identical apartments; heating costs are the same as on Figure 21-7. In each of the following cases, what rent should you charge and how warm should you keep the apartments?

a. Your competitors charge $200/month for similar apartments heated to 68deg..

b. Your competitors charge $180/month for similar apartments heated to 63deg..

c. Your competitors charge $200/month for similar apartments heated to 73deg..

4. I have told you the conclusion of the FTC's analysis of nonrefundable membership contracts for health spas; I have not explained how the conclusion was reached. You know enough economics to do the problem yourself--to show why long-term, nonrefundable contracts are inefficient. Do so. You may make the argument verbal, graphical, or both, as you prefer. (This is a hard problem.)

5. What rate of subsidy should the landlord offer to the tenants of Apartments 2 and 3?

6. Suppose that with electric heating, it is practical for each tenant to control and pay for his own heating; with gas heating, it is not. Tenants have the MV curves shown in Figure 21-11a; the cost of electric heat is shown in Table 21-1. How cheap would gas heating have to be in order for the landlord to prefer gas heating and a uniform temperature to electric heating with subsidies? Express your answer as a ratio between the cost, per unit of heat, of gas heating and of electric heating. (This is a hard problem)

In part 1 of this chapter we ignored the possibility that different houses might be heated with different fuels, or that some homeowners might buy more efficient furnaces than others. If we had included these additional factors, would our conclusion have changed? Discuss.

7. How often does one find a $10 bill lying on the sidewalk? (Hint: The answer is given, for several analogous cases, in the optional section of Chapter 1.)

David Friedman, "Cold Houses in Warm Climates and Vice Versa: A Paradox of Rational Heating." Journal of Political Economy, 1987 , vol. 95, no. 5.