Economics is often thought of either as the answers to a particular set of questions (How do you prevent unemployment? Why are prices rising? How does the banking system work? Will the stock market go up?) or as the method by which such answers are found. Neither description adequately defines economics, both because there are other ways to answer such questions (astrology, for example, might give answers to some of the questions given above, although not necessarily the right answers) and because economists use economics to answer many questions that are not usually considered "economic" (What determines how many children people have? How can crime be controlled? How will governments act?).
I prefer to define economics as a particular way of understanding behavior; what are commonly thought of as economic questions are simply questions for which this way of understanding behavior has proved particularly useful in the past:
Economics is that way of understanding behavior that starts from the assumption that people have objectives and tend to choose the correct way to achieve them.
The second half of the assumption, that people tend to find the correct way to achieve their objectives, is called rationality. This term is somewhat deceptive, since it suggests that the way in which people find the correct way to achieve their objectives is by rational analysis--analyzing evidence, using formal logic to deduce conclusions from assumptions, and so forth. No such assumption about how people find the correct means to achieve their ends is necessary.
One can imagine a variety of other explanations for rational behavior. To take a trivial example, most of our objectives require that we eat occasionally, so as not to die of hunger (exception--if my objective is to be fertilizer). Whether or not people have deduced this fact by logical analysis, those who do not choose to eat are not around to have their behavior analyzed by economists. More generally, evolution may produce people (and other animals) who behave rationally without knowing why. The same result may be produced by a process of trial and error; if you walk to work every day, you may by experiment find the shortest route even if you do not know enough geometry to calculate it. Rationality in this sense does not necessarily require thought. In the final section of this chapter, I give two examples of things that have no minds and yet exhibit rationality.
Half of the assumption in my definition of economics was rationality; the other half was that people have objectives. In order to do much with economics, one must strengthen this part of the assumption somewhat by assuming that people have reasonably simple objectives; with no idea at all about what people's objectives are, it is impossible to make any prediction about what people will do. Any behavior, however peculiar, can be explained by assuming that the behavior itself was the person's objective. (Why did I stand on my head on the table while holding a burning $1,000 bill between my toes? I wanted to stand on my head on the table while holding a burning $1,000 bill between my toes.)
To take a more plausible example of how a somewhat complicated objective can lead to apparently irrational behavior, consider someone who has a choice between two identical products at different prices. It seems that for almost any objective we can think of, he would prefer to buy the less expensive item. If his objective is to help the poor, he can give the money he saves to the poor. If his objective is to help his children, he can spend the money he saves on them. If his objective is to live a life of pleasure and luxury, he can spend the money on Caribbean cruises and caviar.
But suppose you are taking a date to a movie. You know you are going to want a candy bar, which costs $1.00 in the theater and $0.50 in the Seven-Eleven grocery you pass on your way there. Do you stop at the store and buy a candy bar? Do you want your date to think you are a tightwad? You buy the candy bar at the theater, impressing your date (you hope) with the fact that you are the sort of person who does not have to worry about money.
One could get out of this problem by claiming that the two candy bars are not really identical; the candy bar at the theater includes the additional characteristic of impressing your date. But if you follow this line of argument, no two items are identical and the statement that you prefer the lower priced of two identical items has no content. I would prefer to say that the two items are identical enough for our purposes but that in this particular case your objective is sufficiently odd so that our prediction (based on the assumption of reasonably simple objectives) turns out to be wrong.
Economics is based on the assumption that people have reasonably simple objectives and choose the correct means to achieve them. Both halves of the assumption are false; people sometimes have very complicated objectives and they sometimes make mistakes. Why then is the assumption useful?
Suppose we know someone's objective and also know that half the time that person correctly figures out how to achieve it and half the time acts at random. Since there is generally only one right way of doing things (or perhaps a few) but very many wrong ways, the "rational" behavior can be predicted but the "irrational" behavior cannot. If we predict this person's behavior on the assumption that he is rational, we will be right half the time. If we assume he is irrational, we will almost never be right, since we still have to guess which irrational thing he will do. We are better off assuming he is rational and recognizing that we will sometimes be wrong. To put the argument more generally, the tendency to be rational is the consistent (and hence predictable) element in human behavior. The only alternative to assuming rationality (other than giving up and concluding that human behavior cannot be understood and predicted) would be a theory of irrational behavior--a theory that told us not only that someone would not always do the rational thing but also which particular irrational thing he would do. So far as I know, no satisfactory theory of that sort exists.
There are a number of reasons why the assumption of rationality may work better than one would at first think. One is that we are often concerned not with the behavior of a single individual but with the aggregate effect of the behavior of many people. Insofar as the irrational part of their behavior is random, its effects are likely to average out in the aggregate.
Suppose, for example, that the rational thing to do is to buy more hamburger the lower its price. People actually decide how much to buy by first making the rational decision then flipping a coin. If the coin comes up heads, they buy a pound more than they were planning to; if it comes up tails, they buy a pound less. The behavior of each individual will be rather unpredictable, but the total demand for hamburger will be almost exactly the same as without the coin flipping, since on average about half the coins will come up heads and half tails.
A second reason why the assumption works better than one might expect is that we are often dealing not with a random set of people but with people who have been selected for the particular role they are playing. Consider the heads of companies. If you selected people at random for the job, the assumption that they want to maximize the company's profits and know how to do so would not be a very plausible one. But people who do not want to maximize profits, or do not know how to, are unlikely to be chosen for the job; if they are, they are unlikely to keep it; if they do, their companies are likely to become increasingly unimportant in the economy, until eventually the companies go out of business. So the simple assumption of profit maximization plus rationality turns out to be a good way to predict how firms will behave.
A similar argument applies to the stock market. We may reasonably expect that the average investment is made by someone with an accurate idea of what companies are worth--even though the average American, and even the average investor, may be poorly informed about such things. Investors who consistently bet wrong on the stock market soon have very little to bet with. Investors who consistently bet right have an increasing amount of their own money to risk--and often other people's money as well. Hence the well-informed investors have an influence on the market out of proportion to their numbers as a fraction of the population. If we analyze the workings of the market on the assumption that all investors are well informed, we may come up with fairly accurate predictions in spite of the inaccuracy of the assumption. In this as in all other cases, the ultimate test of the method is whether its predictions turn out to describe reality correctly. Whether something is an economic question is not something we know in advance. It is something we discover by trying to use economics to answer it.
So far, I have talked of economics in the abstract; it is now time for some concrete examples. I have chosen examples involving issues not usually considered economic in order to show that economics is not a particular set of questions to be answered but a particular way of answering questions. I will begin with two very simple examples and then go on to some slightly more complicated ones.
You are laying out a college campus as a rectangular pattern of concrete sidewalks with grass between them. You know that one of the objectives of many people, including many students, is to get where they are going with as little effort as possible; you suspect most of them realize that a straight line is the shortest distance between two points. You would be well advised to take precautions against students cutting across the lawn. Possible precautions would be constructing fences or diagonal walkways, adding tough ground cover, or replacing the grass with cement and painting it green.
One point to note. It may be that everyone will be better off if no one cuts across the lawn (assuming the students like to look at green lawns without brown paths across them). Rationality is an assumption about individual behavior, not group behavior. The question of under what circumstances individual rationality does or does not lead to the best results for the group is one of the most interesting questions economics investigates. Even if a student is in favor of green grass, he may correctly argue that his decision to cut across provides more benefit (time saved) than cost (slight damage to the grass) to him. The fact that his decision provides additional costs, but no additional benefits, to other people who also dislike having the grass damaged is irrelevant unless making those other people happy happens to be one of his objectives. The total costs of his action may be greater than the total benefits; but as long as the costs to him are less than the benefits to him, he takes the action. This point will be examined at much greater length in Chapter 18, when we discuss public goods and externalities.
A second simple example of economic thinking is Friedman's Law for Finding Men's Washrooms--"Men's rooms are adjacent, in one of the three dimensions, to ladies' rooms." One of the builder's objectives is to minimize construction costs; it costs more to build two small plumbing stacks (the set of pipes needed for a washroom) than one big one. So it is cheaper to put washrooms close to each other in order to get them on the same stack. That does not imply that two men's rooms on the same floor will be next to each other (although men's rooms on different floors are usually in the same position, making them adjacent vertically).Putting them next to each other reduces the cost, but separating them gets them close to more users. But there is no advantage to having men's and ladies' rooms far apart, since they are used by different people, so they are almost always put on the same stack. The law does not hold for buildings constructed on government contracts at cost plus 10 percent.
As a third example, consider someone making two decisions--what car to buy and what politician to vote for. In either case, the person can improve his decision (make it more likely that he acts in his own interest) by investing time and effort in studying the alternatives. In the case of the car, his decision determines with certainty which car he gets. In the case of the politician, his decision (whom to vote for) changes by one ten-millionth the probability that the candidate he votes for will win. If the candidate would be elected without his vote, he is wasting his time; if the candidate would lose even with his vote, he is also wasting his time. He will rationally choose to invest much more time in the decision of which car to buy--the payoff to him is enormously greater. We expect voting to be characterized by rational ignorance; it is rational to be ignorant when the information costs more than it is worth.
This is much less of a problem for a concentrated interest than for a dispersed one. If you, or your company, receives almost all of the benefit from some proposed law, you may well be willing to invest enough resources in supporting that law (and the politician who wrote it) to have a significant effect on the probability that the law will pass. If the cost of the law is spread among many people, no one of them will find it in his interest to discover what is being done to him and oppose it. Some of the implications of that will be seen in Chapter 19, where we explore the economics of politics.
In the course of this example, I have subtly changed my definition of rationality. Before, it meant making the right decision about what to do--voting for the right politician, for example. Now it means making the right decision about how to decide what to do--collecting information on whom to vote for only if the information is worth more than the cost of collecting it. For many purposes, the first definition is sufficient. The second is necessary where an essential part of the problem is the cost of getting and using information.
A final, and interesting, example is the problem of winning a battle. In modern warfare, many soldiers do not fire their guns in battle, and many of those who fire do not aim. This is not irrational behavior--on the contrary. In many situations, the soldier correctly believes that nothing he can do is very likely to determine who wins the battle; if he shoots, especially if he takes time to aim, he is more likely to get shot himself. The general and the soldier have two objectives in common. Both want their army to win. Both also want the soldier to survive the battle. But the relative importance of the second objective is much greater for the soldier than for the general. Hence the soldier rationally does not do what the general rationally wants him to do.
Interestingly enough, studies of U.S. soldiers in World War II revealed that the soldier most likely to shoot was the member of a squad who was carrying the Browning Automatic Rifle. He was in a situation analogous to that of the concentrated interest; since his weapon was much more powerful than an ordinary rifle (an automatic rifle, like a machine gun, keeps firing as long as you keep the trigger pulled), his actions were much more likely to determine who won--and hence whether he got killed--than the actions of an ordinary rifleman.
The problem is not limited to modern war. The old form of the problem (which still exists in modern armies) is the decision whether to stand and fight or to run away. If you all stand, you will probably win the battle. If everyone else stands and you run, your side may still win the battle and you are less likely to get killed (unless your own side notices what you did and shoots you) than if you fought. If everyone runs, you lose the battle and are quite likely to be killed--but less likely the sooner you start running.
One proverbial solution to this problem is to burn your bridges behind you. You march your army over a bridge, line up on the far side of the river, and burn the bridge. You then point out to your soldiers that if your side loses the battle you will all be killed, so there is no point in running away. Since your troops do not run and the enemy troops (hopefully) do, you win the battle. Of course, if you lose the battle, a lot more people get killed than if you had not burned the bridge.
We all learn in high school history how, during the Revolutionary War, the foolish British dressed their troops in bright scarlet uniforms and marched them around in neat geometric formations, providing easy targets for the heroic Americans. My own guess is that the British knew what they were doing. It was, after all, the same British Army that less than 40 years later defeated the greatest general of the age at Waterloo. I suspect the mistake in the high school history texts is not realizing that what the British were worried about was controlling their own troops. Neat geometric formations make it hard for a soldier to advance to the rear unobtrusively; bright uniforms make it hard for soldiers to hide after their army has been defeated, which lowers the benefit of running away.
The problem of the conflict of interest between the soldier as an individual and the soldiers as a group is nicely illustrated by the story of the battle of Clontarf, as given in Njal Saga. Clontarf was an eleventh century battle between an Irish army on one side and a mixed Irish-Viking army on the other side. The Vikings were led by Sigurd, the Jarl of the Orkney Islands. Sigurd had a battle flag, a raven banner, of which it was said that as long as the flag flew, his army would always go forward, but whoever carried the flag would die.
Sigurd's army was advancing; two men had been killed carrying the banner. The Jarl told a third man to take the banner; the third man refused. After trying unsuccessfully to find someone else to do it, Sigurd remarked, "It is fitting the beggar should bear the bag," cut the banner off the staff, tied it around his own waist, and led the army forward. He was killed and his army defeated. The story illustrates nicely the essential conflict of interest in an army, and the way in which individually rational behavior can prevent victory. If one or two more men had been willing to carry the banner, Sigurd's army might have won the battle--but the banner carriers would not have survived to benefit from the victory.
And you thought economics was about stocks and bonds and the unemployment rate.
PUZZLEYou are a hero with a broken sword (Conan, Boromir, or your favorite Dungeons and Dragons character) being chased by a troop of bad guys (bandits, orcs, . . .). Fortunately you are on a horse and they are not. Unfortunately your horse is tired and they will eventually run you down. Fortunately you have a bow. Unfortunately you have only ten arrows. Fortunately, being a hero, you never miss. Unfortunately there are 40 bad guys. The bad guys are strung out behind you, as shown.
Problem: Use economics to get away.
Note: You cannot talk to the bad guys. They are willing to take a substantial chance of being killed in order to get you--after all, they know you are a hero and are still coming. They know approximately how many arrows you have.
So far, the examples of economic reasoning have not involved any real interaction among the rational acts of different people. We dealt either with a single rational individual--the architect deciding where in the building to put washrooms--or with a group of rational individuals all doing more or less the same thing. Very little in economics is this simple. Before we start developing the framework of price theory in the next chapter, you may find it of interest to think through some more difficult examples of economic reasoning, examples in which the outcome is an equilibrium produced by the interaction of a number of rational individuals.
I will use economics to analyze two familiar situations (supermarket lines and crowded expressways), showing how economics can produce useful and nonobvious results and how the argument can be expanded to deal with successively higher levels of complexity. The logical patterns that appear in these examples reappear again and again in economic analysis. Once you clearly understand when and why supermarket lines are all the same length and lanes in the expressway equally fast, and why and under what circumstances they are not, you will have added to your mental tool kit one of the most useful concepts in economics.
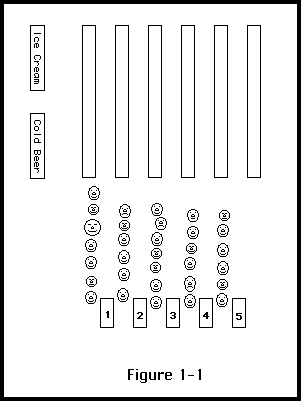
You are standing in a supermarket at the far end of a row of checkout counters with your arms full of groceries. The line at your end blocks your view of the other lines; you know your line is long, but you do not know if the others are any shorter. Should you stagger from line to line looking for the shortest line, or should you get in the nearest one?
The first and simplest answer is that all the lines will be about the same length, so you should get into the one next to you; it is not worth the cost of searching for a shorter one. Why?
Consider any two adjacent lines in Figure 1-1, say Lines 4 and 5. Some shoppers will approach the checkout area not from one end, as you did, but from the aisle that lies between those two lines. Since those shoppers can easily see both lines, they will go to whichever one appears shorter. By doing so, they will lengthen that line and shorten the other; the process continues until both lines are the same length. The same argument holds for every other pair of adjacent lines, so all lines will be the same length. It is not worth it for you to make a costly search for the shortest line.
There are a number of implicit assumptions in this argument. When these assumptions are false the argument may break down. Suppose, for example, that you are at the far end of the row of checkout counters because that is where the ice cream freezer and the refrigerator with the cold beer are located. Many other customers also choose to get these things last and so enter the checkout area from that end. Even if everyone who comes in between Lines 1 and 2 goes to Line 2, there are not enough such people to make Line 2 as long as Line 1. If everyone understands the argument of the previous paragraph and acts accordingly, Line 1 will be longer than Line 2 (and probably much longer than the other lines), and the conclusion of the argument will be wrong.
Imagine that you program a computer to assign customers to lines in a way that equalizes the length of the two lines, as described above, and tell it that 10 people per minute are entering the checkout area at one end (where they can only see Line 1) and 6 per minute are entering between the two lines. The computer informs you that of the 6 customers coming in between the two lines, 8 must go to Line 2 and -2 to Line 1. Since 10 customers are going to Line 1 from the end, the total number going to Line 1 is 10 plus -2, which equals 8--the number going to Line 2. The computer, having solved the problem you gave it, sits there with a satisfied expression on its screen.
You then reprogram it, pointing out that fewer than zero customers cannot go anywhere. Mathematically speaking, you are asking the computer to solve the problem subject to the condition that a certain number (the number of customers coming in between the two lines and going to one of them) cannot be negative. The computer replies that in that case, the best it can do is to send all six customers to Line 2--leaving the lines still unequal.
This sort of result is called a corner solution because it corresponds to the mathematical situation where the maximum of a function is not at the top of its graph but instead at a corner where the graph ends, as shown in Figure 1-2a. In such a situation, the normal conclusion (in the supermarket case, that all the lines must be the same length) may no longer hold. The corresponding result in Figure 1-2a is that the graph is not horizontal at its maximum--as it would be if the maximum were at an interior solution, as it is in Figure 1-2b. In economics--especially mathematical economics--the usual role of corner solutions is to provide annoying exceptions to general theorems.

Supermarket, viewed from above. Lines tend to be equal; Line 1 is a special case because many customers get ice cream and cold beer last.
Are there other situations in which the
conclusion--that all lines will be the same length--does not hold?
Yes.
So far, I have assumed that for people coming in between two lines, it is costless to see which line is shorter. This is not always true. The relevant length, after all, is not in space but in time; you would rather enter a line of ten customers with only a few items each than a line of eight customers with full carts. Estimating which line is shorter requires a certain amount of mental effort. If the system works so well that all lines are exactly the same length (in time), then it will never be worth that effort. Hence no one will make it; hence there will be nothing keeping the lines the same length. In equilibrium the length of lines must differ by just enough to repay (on average) the effort of figuring out which line is shorter. If it differed by more than that, everyone would look for the shortest line, making all lines the same length (assuming no corner solution). If it differed by less than that, nobody would.
It may have occurred to you that I am assuming all customers have the same ability to estimate how long a line will take. Suppose a few customers know that the checker on Line 3 is twice as fast as the others. The experts go to Line 3. Line 3 appears to be longer than the other lines (to nonexperts, that is; allowing for the fast checker, the line is actually shorter, in time although not in length). nonexperts avoid Line 3 until it shrinks back to the same length as the others. The experts (and some lucky nonexperts--the ones who are still in Line 3) get out twice as fast as everyone else.
Word spreads; the number of experts increases. As long as, with all the experts going through Line 3, Line 3 can still be as short (in appearance) as the other lines, the increasing number of experts does not reduce the payoff to being an expert. Every time one more expert enters the line (making it appear slightly longer than the others), one more nonexpert decides not to enter it.
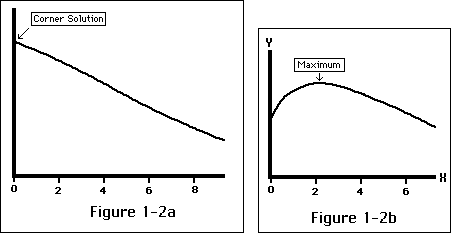
Two maxima--a corner solution (a) and an
interior solution (b). At the interior maximum, the slope of the
curve is zero; at the corner maximum, it need not be.
Eventually the number of experts becomes large enough to crowd out all the nonexperts from that line. As the number of experts increases further, Line 3 begins to lengthen. It cannot be brought back to the same length as the other lines by the defection of nonexperts (who mistakenly believe that it is longer in waiting time as well as length) because there are none of them going to it and the experts know better. Eventually the number of experts becomes so great that Line 3 is twice as long as the other lines and takes the same length of time as they do; the gain from being an expert has now vanished.
To put the same argument in more conventional economic language, rational behavior (in the sense of "making the right decision") requires information. If that information is itself costly, rational behavior consists of acquiring information (paying information costs) only as long as the return from additional information is at least as great as the cost of getting it. If certain minimal information is required to equalize the time-length of lines, then the time-length of lines must be sufficiently unequal so that the saving from knowing which line is shorter just pays the cost of acquiring that information. That principle applies to both the cost of looking at lines to see which is shortest and the cost of studying checkers to learn which ones are faster. The initial argument was given in an approximation in which information was costless; such an approximation greatly simplifies many economic arguments but should be used with care.
There is at least one more hidden assumption in the argument as given. I have assumed that everyone in the grocery store wants to get out as quickly as possible. Suppose the grocery store (Westwood Singles Market) is actually the local social center; people come to stand in long lines gossiping with and about their friends and trying to make new ones. Since they do not want to get out as fast as possible, they do not try to go to the shortest line; so the whole argument breaks down.
A similar analysis can be applied to lanes on the freeway. When you are driving on a crowded highway, it always seems that some other lane is going faster than yours; the obvious strategy is to switch to the faster lane. If you actually try to follow such a strategy, however, you discover to your amazement that a few minutes after you switch lanes, the battered blue pickup that was behind you in the lane you left is now in front of you.
To understand why it is so difficult to follow a successful strategy of lane changing, consider that by moving into a lane you slow it down. If there is a faster lane then people will move into it, equalizing its speed with that of the other lanes, just as people moving into a short line lengthen it. So a lane remains fast only as long as drivers do not realize it is.
Here again, a more sophisticated analysis would allow for the costs (in frayed nerves and dented fenders) of continual lane changes. On average, if everyone is rational, there must be a small gain in speed from changing lanes--if there were not, nobody would do it and the mechanism described above would not work. The payoff must equal the cost for the marginal lane changer--the least well qualified of those following the lane-changing strategy. If the payoff were less than that, he would not be a lane changer; if it were more, someone else would. In principle, if you knew how much a strategy of lane changing cost each driver (in dents and nerves--less for those with strong nerves and old cars) and how many lane changers it took to reduce the benefit from lane changing by any given amount, you could figure out who would be the marginal lane changer and how much the gain from lane changing would be. By the end of the course, you should see how to do this. If you see it now, you are already an economist--whether or not you have studied economics.
Doctors make a lot of money. Doctors also spend many years as medical students and interns. The two facts are not unrelated. Different wages in different professions are set by a process similar to that described above. If one profession is, on net, more attractive than another (taking account of wages, risks, costs of learning the profession, and so on), more people go into the more attractive profession and by so doing drive down the wages. All professions are in some sense equally attractive--to the marginal person. In deciding what profession you want to enter, it is not enough to ask what profession pays the highest wage. Not only are there other factors, there is also reason to expect that the other factors will be worst where the wage is best. What you should ask instead is what profession you are particularly suited for in comparison to other people making similar choices. This is like deciding whether to follow a lane-switching strategy by considering how old your car is compared to others, or deciding whether to look for a shorter line in the grocery store according to how much you are carrying.
A similar argument applies to the stock market. It is often said that if a company is doing very well, you should buy its stock. But if everyone else knows that the company is doing well, then the price of its stock already reflects that information. If buying it were really such a good deal, who would sell? The company you should buy stock in is one that you know is doing better than most other investors think it is--even if in some absolute sense it is not doing very well.
A friend of mine has been investing successfully for several years by following almost the opposite of the conventional wisdom. He looks for companies that are doing very badly and calculates how much their assets would be worth if they went out of business. Occasionally he finds one whose assets are worth more than its stock. He buys stock in such companies, figuring that if they do well their stock will go up and if they do badly they will go out of business, sell off their assets--and the stock will again go up.
If all of this is obvious to you the first time you read it (or even the second), then in your choice of careers you should give serious consideration to becoming an economist.
Several of the situations described in this chapter involved a principle called negative feedback. A familiar example of negative feedback is driving a car. If the car is going to the right of where you want it, you turn the wheel a little to the left; if it is going to the left of where you want, you turn it a little to the right. This is called feedback because an error in the direction you are going "feeds back" into the mechanism that controls your direction (through you to the steering wheel). It is negative feedback because an error in one direction (right) causes a correction in the other direction (left). An example of positive feedback is the shriek when the amplifier attached to a microphone is turned up too high. A small noise comes into the mike, is amplified by the amplifier, comes out of the speaker, and feeds back into the mike. If the amplification is high enough, the noise becomes louder each time around, eventually overloading the system.
In the supermarket line example, the lines are kept at about the same length by negative feedback: If a line gets too long compared to other lines people stop going to it, which makes it get shorter. Similarly, when a lane on the expressway speeds up, cars move into it, slowing it down. In each case, what we are mostly interested in are not the details of the feedback process but rather the nature of the stable equilibrium--the situation such that deviations from it cause correcting feedback.
In defending the assumption of rationality, I pointed out that it is not the same as the assumption that people reason logically. Logical reasoning is not the only, or even the most common, way of getting a correct answer. I will demonstrate this with two extreme examples--cases in which we observe rationality in something that cannot reason, since it has no mind to reason with. In the first case, I will show how a mindless object--a collection of matchboxes filled with marbles--can learn to play a game rationally. In the second, I will show how the rational pursuit of objectives by genes--mindless chains of atoms inside your cells--explains a striking fact about the real world, something so fundamental that it never occurs to most of us to find it surprising.
Suppose you want to build a computer to play some simple game, such as tic-tac-toe. One way is to build in the correct move for every situation. Another, and in some ways more interesting, approach is to let the computer teach itself how to play. Such a learning computer starts out moving randomly. Each time a game ends, the computer is told whether it won or lost and adjusts its strategy accordingly, lowering the probability of moves that led to losses and increasing the probability of moves that led to wins. After enough games, the computer may become a fairly good player.
The computer does not think. Its "mind" is simply a device that identifies the present situation of the game, chooses a move by some random mechanism, and later adjusts the probabilities according to whether it won or lost. A simple version consists of a bunch of matchboxes filled with black and white marbles, laid out on a diagram of the game. Moves are chosen by picking a marble at random, with the color of the marble determining the move. The mix of marbles in each matchbox is adjusted at the end of the game to make moves that led to a win more likely and moves that led to a loss less likely.
A matchbox computer, or its more sophisticated electronic descendants, does not think, yet it is rational. Its objective is to win the game and, after it has played long enough to "learn" how to win, it tends to choose the correct way of achieving that objective. We can understand and predict its behavior in the same way that we understand and predict the behavior of humans. "Rationality" is simply the ability to get the right answer; it may be the result of many things other than rational thinking.
There is a close historical connection between economics and evolution. Both of the discoverers of the theory of evolution (Darwin and Wallace) said they got the idea from Thomas Malthus, an economist who was also one of the originators of the so-called Ricardian Theory of Rent (named after David Ricardo, who used it but did not invent it), one of the basic building blocks of modern economics.
There is also a close similarity in the logical structure of the two fields. The economist expects people to choose correctly how to achieve their objectives but is not very much concerned with the psychological question of how they do so. The evolutionary biologist expects genes--the fundamental units of heredity that control the construction of our bodies--to construct animals whose structure and behavior are such as to maximize their reproductive success (roughly speaking, the number of their descendants), since the animals that presently exist are descended from those that were reproductively successful in the past and carry the genes that made them successful. The biologist need not be concerned very much with the detailed biochemical mechanisms by which the genes control the organism. Many of the same patterns appear in both economics and evolutionary biology; the conflict between individual interest and group interest that I mentioned earlier reappears in the conflict between the interest of the gene and the interest of the species.
A nice example is Sir R.A. Fisher's explanation of observed sex ratios. In many species, including ours, male and female offspring are produced in roughly equal numbers. There is no obvious reason why this is in the interest of the species; one male suffices to fertilize many females. Yet the sex ratio remains about 1:1, even in some species in which only a small fraction of the males succeed in reproducing. Why?
Fisher's answer is as follows. Imagine that two thirds of offspring are female, as shown in Figure 1-3. Consider three generations. Since each individual in the third generation has both a father and a mother, if there are twice as many females as males in the second generation, the average male must have twice as many children as the average female. This means that an individual in the first generation who produces a son will, on average, have twice as many grandchildren as one who produces a daughter. Individual A on Figure 1-3, for example, has six children, while Individual B only has three. A's parents got twice as great a return in grandchildren for producing A as B's parents did for producing B.
If there are more females than males in the population, couples who produce sons have more descendants, on average, than those who produce daughters. Since couples who produce sons have more descendants, more of the population is descended from them and has their genes--including the gene for having sons. Genes for producing male offspring increase in the population.
The initial situation, in which two thirds of the population in each generation was female, is unstable. As long as more than half of the children are female, genes for having male children spread faster than genes for having female children; so the percentage of female children falls. Similarly, if more than half the children were male, genes for having female children would have the advantage and spread. Either way, the situation must swing back towards an even sex ratio.
In making this argument, I implicitly assumed equal cost for producing male and female offspring. In a species with substantial sexual dimorphism (male and female babies of different size), the argument implies that the total weight of female offspring (weight per offspring times number of offspring) will be about the same as that for male offspring. One could add further complications by considering differences in the costs of raising male and female offspring to maturity. Yet even the simple argument is strikingly successful in explaining one of the observed regularities of the world around us by the "rational" behavior of microscopic entities. Genes cannot think--yet in this case and many others, they behave as if they had carefully calculated how to maximize their own survival in future generations.
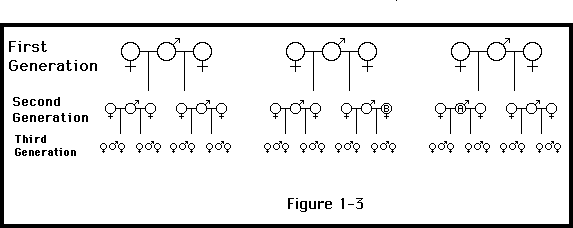
Three generations of a population with a male:female ration of 1:2. Members of the first generation who have a son produce twice as many grandchildren as those who have a daughter, so genes for having sons increase in the population, swinging the sex ratio back toward 1:1.
1. In defending the rationality assumption, I argued that while people sometimes make mistakes, their correct decisions are predictable and their mistakes are not. Can you think of any alternative approaches to understanding human behavior that claim to predict the mistakes? Discuss.
2. Give examples (other than buying candy for your date--the example discussed in the text) of apparently irrational behavior that consists of choosing the correct means to achieve an odd or complicated end.
3. In this chapter and throughout the book I treat individual preferences as givens--I neither judge whether people have the "right" preferences nor consider the possibility that something might change individual preferences.
a. Do you think some preferences are better than others? Give examples. Discuss.
b. Describe activites that you believe can only be understood as attempts to change people's preferences. How would you try to analyze such activities in economic terms?
4. Friedman's Law for Finding Men's Washrooms could be described as fossilized rationality--whether the architect lives or dies, his rationality remains set in concrete in the building he designed.
a. Can you think of other examples? Discuss.
b. Can you describe any cases where instead of deducing the shape of something from the rationality of its maker, we deduce the rationality of its maker from its shape? Discuss.
5. What devices (other than those discussed in the text) are used by generals, ancient and modern, to prevent soldiers from concluding that it is in their interest to run away, not aim, or in some other way act against the interest of the army of which they are a part?
6. The problem I have discussed exists not only in your army but in the enemy's army as well. Discuss ways in which a general might take advantage of that fact, giving real-world examples if possible.
7. In a recent conversation with one of our deans, I commented that I was rather absent-minded--I had missed two or three faculty meetings that year--and wished I could get him to make a point of reminding me when I was supposed to be somewhere. He replied that he had already solved that problem, so far as the (luncheon) meetings he was responsible for. He made sure I would not forget them by always arranging to have a scrumptious chocolate dessert.
a. Is this an economic solution to the problem of getting me to remember things? Discuss.
b. In what sense does or does not the success of this method indicate that I "choose" to forget to go to meetings? Discuss.
8. This chapter discusses situations where rational behavior by each individual leads to results that are undesirable for all. Give an example of such a situation in your own experience; it should not be one discussed in the chapter.
9. Many voters are rationally ignorant of the names of their congressmen. List some things you are rationally ignorant of. Explain why your ignorance is rational. Extra credit if they are things that many people would say you ought to know.
The following problems refer to the optional section:
10. The analyses of supermarket lines, freeway lanes, and the stock market all had the same form. In each case, the argument could be summarized as "The outcome has a particular pattern because if it did not, it would be in the interest of people to change their behavior in a way that would push the outcome closer to fitting the pattern." Such a situation is called a stable equilibrium. Can you think of any examples not discussed in the text?
11. Analyze express lanes in supermarkets. Is the express lane always faster? If not, when is it and when is it not?
12. In the supermarket example, I started by assuming that you had your arms full of groceries. Why? How does that assumption simplify the argument?
13. The friend whose investment strategy I described is a very talented accountant. When I met him, he was in his early twenties and was making a good income teaching accounting to people who wanted to pass the CPA exam. Does this have anything to do with his investment strategy?
14. Is there any reason why my accountant friend should prefer that this book, or at least this chapter, not be published?
15. Give some examples of negative and positive feedback in your own experience.
16. Certain professions are very attractive to their members and very badly paid. Consider the stereotype of the starving artist--or a friend of mine who is working part-time as a store clerk while trying to make a career as a professional lutenist. Is the association between job attractiveness and low pay accidental, or is there a logical connection? Discuss.
17. You have been collecting data on the behavior of a particular stock over many years. You notice that every Friday the 13th, the stock drops substantially, only to come back up over the next few weeks; your conclusion is that superstitious stockholders sell their stock in anticipation of bad luck. What can you do to make use of this information? What effect does your action have? Suppose more people notice the behavior of the stock and react accordingly; what is the effect?
18. Generalize your answer to the previous question to cover other situations where a stock price changes in a predictable way. What does this suggest about schemes to make money by charting stock movements and using the result to predict when the market will go up?
19. Suppose that in Floritania the total cost of bringing up a son is three times the cost of bringing up a daughter, since Floritanians do not believe in educating women. Floritanians simply love grandchildren; every couple wants to have as many as possible. Due to a combination of modern science and ancient witchcraft, Floritanian parents can control the gender of their offspring. What is the male/female ratio in the Floritanian population? Explain.
20. The principal foods of the Floritanians are green eggs and ham. It costs exactly twice as much to produce a pound of green eggs as a pound of ham. The more green eggs that are produced, the lower the price they sell for, and similarly with ham.
a. You are producing both green eggs and ham. Green eggs sell for $3/pound; so does ham. How could you increase your revenue without changing your production cost?
b. What will be the result on the prices of green eggs and ham?
c. If everyone acts rationally, what can you say about the eventual prices of green eggs and ham in Floritania?
For a good introduction to the economics of genes I recommend Richard Dawkins's The Selfish Gene (New York: Oxford University Press, 1976).
A more extensive discussion of the economics of warfare can be found in my essay, "The Economics of War," in J.E. Pournelle (ed.), Blood and Iron (New York: Tom Doherty Associates, 1984).
For a very different application of economic analysis to warfare, I recommend Donald W. Engels's Alexander the Great and the Logistics of the Macedonian Army (Berkeley: University of California Press, 1978). The author analyzes Alexander's campaigns while omitting all of the battles. His central interest is in the problem of preventing a large army from dying of hunger or thirst and the way in which that problem determined much of Alexander's strategy. Consider, as a very simple example, the fact that you cannot draw water from a well, or 5 wells, or 20 wells, fast enough to keep an army of 100,000 people from dying of thirst.
The relationship between individual rationality and group behavior is analyzed in Thomas Schelling's Micromotives and Macrobehavior (New York: W.W. Norton and Co., 1978).