Several chapters back, I described the economy as a complicated interdependent system and proposed to solve it by separately solving the parts. I have now done so, at least for a simple economy. The separate pieces are the consumer, the producer, and the market in which they interact. In discussing the consumer's behavior, in Chapters 3 and 4, we saw how the attempt to achieve his objectives leads to an individual demand curve, describing how much he will buy of a good at any price. The shape of this demand curve depends on the preferences of the individual, his income, and the prices of all other goods. Once we have the individual demand curves, we can sum them to get a market demand curve.
In Chapter 5, we saw how a similar argument leads to a supply curve. One new element was the addition of a production function--a relation between the time a particular producer spends producing things and how much he produces. In Chapter 5, the production function took the form of a table showing the rates at which a producer could produce each of various combinations of goods. The producer could use his time to produce goods, sell the goods for money, and, as a consumer, use the money to buy the goods he wished to consume.
Here, as in most of economics, money is not essential to the analysis, although it makes its presentation easier. We could analyze production and consumption in essentially the same way even if all trade occurred by barter, with individuals producing goods and exchanging them directly for other goods. The only difference would be that the system would appear more complicated, both to us and to the people inside it. Instead of talking about the price of apples, or meals, or lawn mowing, we would have to talk about the price of apples measured in meals or the price of lawn mowing measured in oranges; this would complicate both our description of the economy and the lives of the participants.
Another complication of barter, from the standpoint of individual traders, is the double coincidence problem. In an economy with money, an individual can sell the goods he produces to one person and use the money to buy what he wants from another. In a barter economy, the trader must find one person who both has what he wants and wants what he has. In almost all of the analysis so far, I have neglected the transaction costs associated with a market--the costs of finding someone to trade with and negotiating an exchange. That useful simplification would be less plausible in a barter market.
Having gotten demand curves (and consumer surplus) from the chapters on consumption, and supply curves (and producer surplus) from the chapter on production, we combined the two in Chapter 7 to describe how market prices are determined, how they are affected by changes in supply and demand, and the effects of the resulting changes in price and quantity on the welfare of consumers and producers. We now have all the pieces of an economy--supply, demand, and their combination. Let us see if we can assemble them.
Putting the pieces together appears very simple. We start with individual preferences, represented by indifference curves or utility functions, and the ability of individuals to produce goods--production functions. The preferences of consumers (and their incomes) give us demand curves, the preferences of producers (between leisure and income) plus production functions give us supply curves, the intersections of supply and demand curves give us prices (and quantities), and we are finished. We have derived prices and quantities from preferences and production functions.
It is not so simple. The intersection of supply and demand curves gives us prices. Prices (of the goods the individuals produce and sell) give us incomes. But we needed incomes to start with, since they were one of the things that determined demand curves!
The same problem appears if we stop talking about prices in general and talk instead about particular prices. We run through our supply and demand argument to get the price of widgets. We then do the same to get the price of cookies. But one of the things affecting the demand for widgets is the price of cookies (if cookies are inexpensive, you spend your money on them instead of on widgets). We could solve that problem by solving for cookies first--but one of the things affecting the demand for cookies might well be the price of widgets.
Why would we expect the demand curve for one good to depend on the price of another? There are two reasons. The first is that the goods may actually be related in consumption; this is the case of what are called complements and substitutes. Bread and butter, for example, are commonly used together, so the value of bread to you depends in part on the price of butter, and vice versa. Your demand curve for bread goes up when the price of butter goes down. Bread and butter are complements. Trains and airplanes both provide the same service--transportation. Your demand curve for rail travel goes down when airline fares go down. Trains and airplanes are substitutes.
These possibilities may be assumed away when we are trying to describe a very simple economy. We can limit our analysis, as we did in most of Chapter 4, to people for whom the usefulness of one good never depends on how much they have of another, and then reintroduce such complications at a later stage of the analysis. We may assume, in other words, that the individual's utility function is simply the sum of a lot of little utility functions--utility of apples (which depends only on how many apples he has) plus utility of oranges plus utility of water plus . . . . There is a second sort of interdependence which cannot be dealt with so easily. The demand curve of a good is identical to its marginal value curve, which tells us how many dollars are equivalent to a little more of the good. But dollars are valuable for the (other) goods that they can buy, so the value of a dollar depends on the price of those goods. If all prices go down, a unit of a good is still equivalent to the same amount of some other good but to fewer dollars; so the demand curve for one good depends on the prices of the other goods that money could be spent on. As I have pointed out before, a drop in the price of everything is just like an increase in income--and has similar effects on the demand curve for any particular thing.
In thinking about what determines the price of one good, it is convenient, and often correct, to treat all other prices as given and work through the effect of some change in demand or supply on the particular good we are interested in. We cannot follow the same procedure in understanding the whole interdependent system. Each price depends on all other prices, both directly, because the price of one good to a consumer may affect his demand curve for other goods, and indirectly, since the price of a good to its producer affects his real income, which in turn affects his supply and demand curves for other goods.
The interdependence of the different elements that make up the economic system is not wholly new; it is a more complicated example of a problem we have already met and dealt with. The error is in thinking that, having worked out the separate parts of the problem, we can then assemble them one part at a time--solve for one part of the system, then for another, then . . . . The discussion of the egg market in Chapter 7 started with a simpler form of the same mistake. I tried to solve the problem in a series of stages; at each stage, I solved part of the system while ignoring its effect on the rest. I started with a given quantity of eggs being produced, then found the price at which that was the quantity consumers wished to consume. At that point, I was solving for price, given the requirement that price must be such that quantity demanded (at that price) equals quantity produced. I next found the quantity that would be produced at that price; in other words, I solved for quantity, given the condition that quantity produced must be the quantity producers choose to produce, using the price derived in the previous stage of the argument. That gave me a different quantity produced, which had to be plugged back into the demand side of the analysis (the first step), yielding a different price, which must be plugged back into the supply side, yielding a different quantity ... . The logical tangle that results is a (simple!) case of an attempt to solve an interacting system one piece at a time while ignoring the effect on all the other pieces.
The solution was to stop treating it as a mechanism and instead look for the equilibrium point. That occurs at the one price and quantity combination for which quantity supplied equals quantity demanded. In the more complicated case of the whole economy, we will follow essentially the same procedure.
Our problem is to start with individual preferences and productive abilities and derive a complete set of equilibrium prices and quantities. The first step is to consider some list of prices--a price for every good. This initial list is simply a first guess, a set of prices chosen at random.
Since each supply curve is determined by the prices of the goods the producer would like to buy and of the other goods he could sell (and preferences and production functions, which we know), we can calculate all supply curves. Since quantity supplied of any good is determined by the supply curve and the price of that good, we can calculate the quantity supplied of every good. Since income is determined by the prices of the goods we produce and the quantities we produce of them, we can calculate every producer's income. Since the demand curve for any particular good is determined by income (of the consumers, which they get as producers) and prices (of other goods), we can calculate all demand curves; since quantity demanded of any good is determined by the demand curve and the price of that good, we can calculate the quantity demanded of every good.
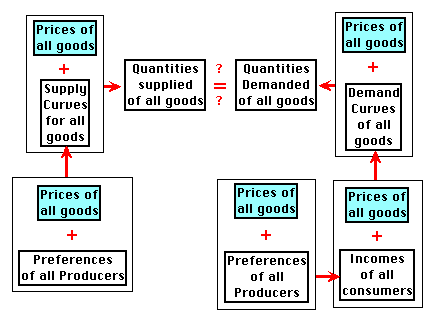
So, starting with preferences, production functions, and a list of prices, we can calculate all quantities supplied and demanded and compare the quantity demanded of every good with the quantity supplied. If the two are equal (for every good), we have the right list of prices--the list that describes the equilibrium of the system. If they are not equal, we pick another list of prices and go through the calculation again. We continue until we find the right list of prices. The logical sequence is diagrammed in Figure 8-1.
In practice, this would be a slow way of finding the right answer, rather like putting a thousand monkeys at a thousand typewriters and waiting for one of them to type out Hamlet by pure chance. After the first million years, they might have produced nothing better than "To be or not to be, that is the grglflx." There are faster ways, provided you have explicit descriptions of everybody's preferences and productive abilities; the general mathematical problem is that of solving a set of n equations in n unknowns. Our simple egg example was a problem of two equations (quantity equals quantity producers choose to supply at the price; quantity equals quantity demanded at the price) in two unknowns (quantity and price). A problem with two unknowns can be solved in two dimensions, which happened to be the number we had available, so we were able to solve the problem graphically by finding the point where two lines (the supply and demand curves) intersected.
I have gone through right and wrong ways of solving an economy so fast that you may have lost the former in the latter. I will therefore repeat the very simple result.
To solve an economy, find that set of prices such that quantity demanded equals quantity supplied for all goods and services.
That simple result--contrasted with the previous hundred and some pages--may remind you of the mountain that gave birth to a mouse. But without those pages, we would not have known how prices (and preferences) generate supply and demand curves, nor how supply and demand curves in turn determine prices.
Solving even a very simple real-world economy would involve thousands of equations; in practice, the problem is insoluble even with advanced mathematics and modem computers. But the point of the analysis is not actually to solve an economy and come up with a set of prices and quantities. Even if we knew how to solve the equations we could not write them down in the first place, since we do not know everyone's preferences and abilities. What we observe are prices and quantities; we see the solution, not the problem. The point of the analysis is to learn how the system is interrelated, so that we can understand how any particular change (a tariff, a tax, a law, an invention) affects the whole system. Also for the fun of understanding the logical structure of the interrelated world around us.
Your response may be that we do not understand a system if our "solution" requires information and calculating abilities we do not have. But as I tried to make clear in Chapter 1, economists do not expect to know what people's objectives are, only what the consequences are of people rationally pursuing them. Nor, I might have added, are economists experts in the technology of production.
If you think economics is useless if it cannot actually solve an economy--predict what the entire set of prices and quantities is going to be--consider what we have already done. The book so far contains demonstrations of at least four strikingly counterintuitive results: (1) that a theater owner maximizes his profit by selling popcorn at cost, (2) that for a nation or individual to be better at producing one thing is logically equivalent to its being worse at producing something else (the principle of comparative advantage), (3) that the costs imposed by taxes on producers and consumers are unaffected by who pays the taxes, and (4) that legal restrictions on leases "in favor of tenants" either have no effect or hurt both tenants and landlords. Not one of those conclusions depended on our knowing any real-world demand or supply curve, nor any of the preferences and abilities from which those curves might have been derived.

How to solve an economy. Starting with prices of all goods, production functions,
and preferences of all consumers, one can derive quantities supplied
and demanded. If they are equal for all goods, the initial set of
prices describes a possible market equilibrium--a solution for that
economy.
Economics is not the only science that analyzes systems it cannot actually solve. The three-body problem--the problem of determining the behavior of three objects interacting by gravitational attraction according to the laws of Newtonian physics--has not yet been solved, but that does not prevent astronomers from studying the solar system, which contains at least nine planets, the sun, and a considerable number of moons, comets, and asteroids.
The kind of economics that we did in Chapter 7 is what economists call partial equilibrium analysis; we analyzed the effect of changes in the market for one good, whether widgets or apartments, while ignoring the effects on other goods. The kind of economics that we did in this chapter, when we saw how, in principle, an economy can be solved, is called general equilibrium analysis.
Most economic analysis, in this book and elsewhere, is partial equilibrium; one assumes that the effects one is interested in are limited to one or at most a few goods. In many situations, this is a legitimate assumption--not because it is precisely correct but because it leads to correct conclusions.
Consider a change that shifts the demand or supply curve for one good. The result is to change the price of the good and the quantity produced and purchased, as described in Chapter 7. It is very unlikely that, after the change, each consumer will be spending the same amount of money on the good at the new price as he did at the old.
If a consumer is spending more (or less) on the good whose price has changed, he must be spending less (or more) on all other goods. Hence the quantity demanded of those goods has changed. Hence the initial assumption, that only the one good was affected, is wrong.
It is wrong but, like the assumptions on which economics is built, useful. In most cases, such effects are spread among a large number of other goods, each of which is only slightly affected (this is not true in the special case of two goods that are close substitutes or close complements, which is why such goods must be treated together in such an analysis). Small changes in prices generally produce very small effects on total surplus--the sum of consumer and producer surplus. Roughly speaking, a $0.10 increase in price produces not one tenth the effect of a $1 increase but one hundredth. The reason is that when a price goes up, most of the resulting loss in consumer's surplus is a gain in producer surplus; only that part of the loss of (consumer and producer) surplus associated with the reduction in quantity produced and consumed is a net loss. Since the reduction in quantity associated with a price increase of $1 is about 10 times as great as that associated with a price increase of $0.10 (exactly 10 times if the relevant curve is a straight line) and since the average consumer surplus per unit on the lost consumption is also about 10 times as high, the product is 100 times as great.
It follows from this argument that while it may be important that a change in the price and quantity of one good results in a change of $1 in the price of another good, it is much less important if the change in one good results in a change of $0.10 in 10 other goods, and still less if it results in a $0.01 change in each of 100 other goods. Since such effects are typically spread over thousands of goods, it is usually legitimate to ignore them. This is one justification for using partial equilibrium analysis. The reason for doing so is that, as you have probably realized at this point, general equilibrium analysis is usually much harder.
I have spent most of this chapter showing that the way in which we have been doing economics is not quite correct, explaining what the correct way would be, and then explaining why I am going to keep on using the "not quite correct but much easier" approach. It would seem that if I omitted the whole discussion, the book could continue in exactly the same way, saving the reader a chapter of work and a considerable amount of confusion. In that sense, this chapter is unnecessary; there is not a single problem anywhere else in the book that depends on understanding this chapter for its solution--and this chapter has no problems.
The justification for this chapter--and complications elsewhere that may seem equally unnecessary--is my belief that lying to students is bad pedagogy. If I am going to teach you a particular way of doing economic analysis, I ought to point out its problems and inconsistencies--as I have done in this chapter--instead of passing quietly over them in the hope that you will not notice. The argument by which I have tried to justify the way in which I am doing economics is really only a sketch of a much more complicated argument, one that those of you who decide to become economists will probably encounter again in a few years. In the rest of this book, I will limit myself to partial equilibrium theory; the purpose of this chapter was to explain why.